
科目: 来源: 题型:
【题目】在△ABC 与△DEF 中,下列四个命题是真命题的个数共有( )
①如果A D, ![]() ,那么△ABC 与△DEF相似;
,那么△ABC 与△DEF相似;
②如果A D,![]() ,那么△ABC 与△DEF相似;
,那么△ABC 与△DEF相似;
③如果A D 90°,![]() ,那么△ABC 与△DEF相似;
,那么△ABC 与△DEF相似;
④如果A D 90°, ![]() ,那么△ABC 与△DEF相似.
,那么△ABC 与△DEF相似.
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值是_______.
的值是_______.
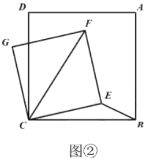
(2)如图②,在正方形![]() 中,
中,![]() ,点
,点![]() 是平面上一动点,且
是平面上一动点,且![]() ,连接
,连接![]() ,在
,在![]() 上方作正方形
上方作正方形![]() ,求线段
,求线段![]() 的最大值.
的最大值.
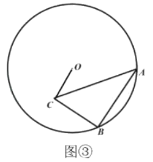
问题解决:(3)如图③,![]() 半径为6,在
半径为6,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 内,且
内,且![]() .当点
.当点![]() 在圆上运动时,求线段
在圆上运动时,求线段![]() 的最小值.
的最小值.
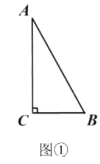
查看答案和解析>>
科目: 来源: 题型:
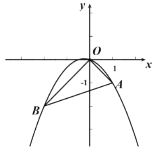
【题目】如图,二次函数![]() 的图像经过
的图像经过![]() 的三个顶点,其中
的三个顶点,其中![]() ,
,![]()
(1)求点![]() 的坐标;
的坐标;
(2)在第三象限存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,求满足条件的点
为顶点的四边形是平行四边形,求满足条件的点![]() 的坐标;
的坐标;
(3)在(2)的条件下,能否将抛物线![]() 平移后经过
平移后经过![]() 两点,若能求出平移后经过
两点,若能求出平移后经过![]() 两点的拋物线的表达式,并写出平移过程.若不能,请说明理由.
两点的拋物线的表达式,并写出平移过程.若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了丰富校园生活,展现同学们英语表达的风采,某校组织了“英语风采大赛”,大赛共设置四个比赛项目.八年级六班的同学们踊跃报名,在“才艺表演”项目中,小怡报名表演古筝,小宏报名表演小提琴,小童报名表演笛子,小灿和小源报名唱英文歌曲.为了取得良好的节目效果,体现公平公正.文体委员决定采用以下方法搭配组合节目:制作5张完全相同的卡片,正面分别写上报名参加比赛同学的姓名,将卡片反面朝上洗匀,然后随机抽取卡片,卡片正面是谁的名字,谁就代表班级参加比赛.
(1)随机抽取一张卡片,求六班才艺表演项目是“乐器独奏”的概率;
(2)随机抽取两张卡片,请用树状图或列表法求小宏和小灿组合参加比赛的概率.(注:可以用![]() 分别表示小怡,小宏,小童,小灿,小源的名字)
分别表示小怡,小宏,小童,小灿,小源的名字)
查看答案和解析>>
科目: 来源: 题型:
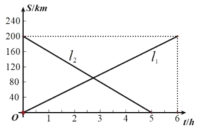
【题目】已知![]() 两地相距
两地相距![]() ,甲、乙两辆货车装满货物分别从
,甲、乙两辆货车装满货物分别从![]() 两地相向而行,图中
两地相向而行,图中![]() 分别表示甲、乙两辆货车离
分别表示甲、乙两辆货车离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数关系.请你根据以上信息,解答下列问题:
之间的函数关系.请你根据以上信息,解答下列问题:
(1)分别求出直线![]() 所对应的函数关系式;
所对应的函数关系式;
(2)何时甲货车离![]() 地的距离大于乙货车离
地的距离大于乙货车离![]() 地的距离?
地的距离?
查看答案和解析>>
科目: 来源: 题型:
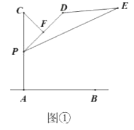
【题目】在炎热的夏季,遮阳伞在我们的生活中随处可见.如图①,滑动调节式遮阳伞的立柱![]() 直于地面
直于地面![]() ,点
,点![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() .当点
.当点![]() 位于初始位置
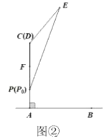
位于初始位置![]() 时,点
时,点![]() 与
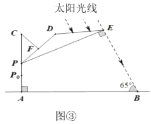
与![]() 重合(如图②).根据生活经验,当太阳光线与
重合(如图②).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.已知太阳光线与地面的夹角为
垂直时,遮阳效果最佳.已知太阳光线与地面的夹角为![]() (如图③),为使遮阳效果最佳,点
(如图③),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少米?(结果精确到
上调多少米?(结果精确到![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目: 来源: 题型:
【题目】2020年伊始,全国发生了传播速度快、感染范围广、防控难度大的新冠肺炎疫情.根据教育部提出的2020年春节延期开学,“停课不停学”的相关要求,很多学校开展了线上授课相关工作.为了更好地提高学生线上授课的效果,某中学进行了线上授课问卷调查.其中一项调查是:你认为影响师生互动的最主要因素是A.教师的授课理念;B.网络配麦等硬件问题;C.科目特点;D.学生的配合情况,针对这个题目,问卷时要求每位同学必须且只能选择其中一项.现随机抽取了若干名学生的调查问卷,将所得数据进行整理,制成如下条形统计图和扇形统计图.
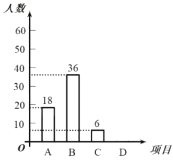
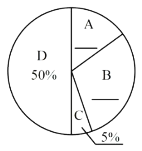
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生中认为影响师生互动最主要因素的众数为____________;
(3)已知该校有2400名学生,请你估计该校学生中认为影响师生互动的最主要因素是“C.科目特点”的有多少人?
查看答案和解析>>
科目: 来源: 题型:
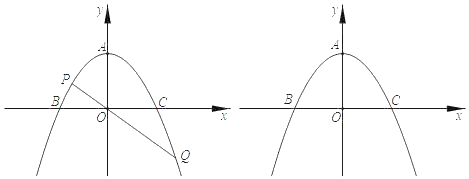
【题目】已知:如图,抛物线![]() 的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=2OP.若点Q正好落在该抛物线上,求点P的坐标;
(3)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=mOP(m为常数);
①证明点Q一定落在抛物线![]() 上;
上;
②设有一个边长为m+1的正方形(其中m>3),它的一组对边垂直于x轴,另一组对边垂直于y轴,并且该正方形四个顶点正好落在抛物线![]() 和
和![]() 组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
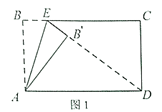
【题目】已知矩形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() 、
、![]() 重合),如图1所示,沿折痕
重合),如图1所示,沿折痕![]() 翻折得到
翻折得到![]() ,设
,设![]() .
.
(1)当![]() 、
、![]() 、
、![]() 在同一直线上时,求
在同一直线上时,求![]() 的值;
的值;
(2)如图2,点![]() 在
在![]() 边上,沿
边上,沿![]() 再次折叠纸片,使点
再次折叠纸片,使点![]() 的对应点
的对应点![]() 在直线
在直线![]() 上,
上,
①求![]() 的最小值;
的最小值;
②点![]() 能否落在边
能否落在边![]() 上?若能,求出
上?若能,求出![]() 的值,若不能,试说明理由.
的值,若不能,试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com