
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+c(a≠0)的图象经过点B (4,0)、D (5,3),设它与x轴的另一个交点为A(点A在点B的左侧),且△ABD的面积是3.
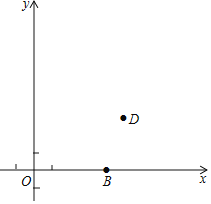
(1)求该抛物线的表达式;
(2)求∠ADB的正切值;
(3)若抛物线与y轴交于点C,直线CD交x轴于点E,点P在射线AD上,当△APE与△ABD相似时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在△ABC中,点D、E分别在边BC和AB上,且AD=AC,EB=ED,分别延长ED、AC交于点F.

(1)求证:△ABD∽△FDC;
(2)求证:AE2=BEEF.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
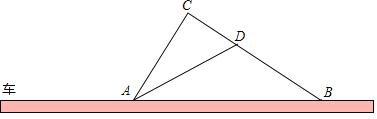
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,反比例函数的图象经过点A、P,点A(6,![]() ),点P的横坐标是2.抛物线y=ax2+bx+c(a≠0)经过坐标原点,且与x轴交于点B,顶点为P.
),点P的横坐标是2.抛物线y=ax2+bx+c(a≠0)经过坐标原点,且与x轴交于点B,顶点为P.
求:(1)反比例函数的解析式;
(2)抛物线的表达式及B点坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】当前,商丘市正在围绕打响“游商丘古都城,读华夏文明史”文化旅游品牌,加快推进商丘景点保护性修复与宣传工作,以此带动以文化为核心的全域旅游跨越发展,打造华夏历史文明商丘传承创新区.随着社会经济的发展和城市周边交通状况的改善,旅游已成为人们的一种生活时尚,某中学开展以“我最喜欢的商丘风景区”为主题的调查活动,围绕“在森林公园、日月湖、汉梁公园和睢阳古城”四个风景区中,你最喜欢哪一个?(必选且只选一个)”的问题,在全校范围内随机抽取了部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
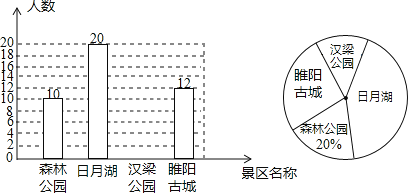
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若该中学共有3000名学生,请你估计最喜欢日月湖风景区的学生有多少名.
查看答案和解析>>
科目: 来源: 题型:
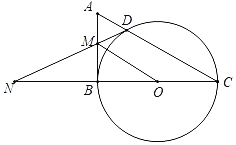
【题目】如图,在Rt△ABC中,以BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点M,交CB延长线于点N,连接OM,OC=1.
(1)求证:AM=MD;
(2)填空:
①若DN![]() ,则△ABC的面积为 ;
,则△ABC的面积为 ;
②当四边形COMD为平行四边形时,∠C的度数为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】“马踏飞燕”作为商丘的地标性雕塑被拆分为两座雕塑,安放在紧邻高速公路出站口的平原路和华商大道交叉口,不光临近古城景区,也靠近火神台,恰恰实现了商丘市的城市文化宣传的目的.“人们来到商丘,一下高速,就看到商丘的地标,就能够感受到商丘的火文化.”
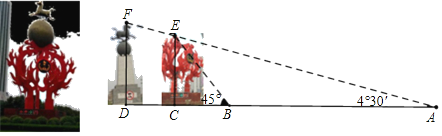
某中学数学兴趣小组准备测量安放后的雕塑相关数据,如图,小明从A点测得“火球”最高点E的仰角为4°30′,此处恰好看不到“马踏飞燕”雕塑的最高点F,小明向雕塑走140m到达点B,此时测得点E的仰角为45°.已知两雕塑的距离为50m,求两座雕塑EC、FD的高度.(A、B、C、D在同一直线上)(精确到1m,参考值:sin4°30′≈0.07,cos4°30′≈0.99,tan4°30′≈0.08.)
查看答案和解析>>
科目: 来源: 题型:
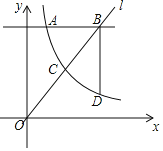
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(1)求反比例函数的解析式;
(2)当BD=2AB时,求点B的坐标;
(3)在(2)的条件下,直接写出不等式![]() >mx的解集.
>mx的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】商丘市梁园区紧紧围绕十九大报告提出的阶段性目标任务,深化农业供给侧结构性改革,调整种植结构,深入进行了四大结构调整,分别是:水池铺乡的辣椒产业、刘口乡的杂果基地,孙福集乡的山药、莲藕产业,双八镇的草莓产业.目前,这四种产业享誉省内外.
某外地客商慕名来商丘考查,他准备购入山药和草莓进行试销,经市场调查,若购进山药和草莓各2箱共花费170元,购进山药3箱和草莓4箱共花费300元.
(1)求购进山药和草莓的单价;
(2)若该客商购进了山药和草莓共1000箱,其中山药销售单价为60元,草莓的销售单价为70元.设购进山药x箱,获得总利润为y元.
①求y关于x的函数关系式;
②由于草莓的保鲜期较短,该客商购进草莓箱数不超过山药箱数的![]() ,要使销售这批山药和草莓的利润最大,请你帮该客商设计一个进货方案,并求出其所获利润的最大值.
,要使销售这批山药和草莓的利润最大,请你帮该客商设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目: 来源: 题型:
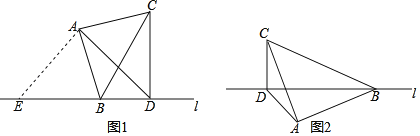
【题目】如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.
(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为 °,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为 ;
(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;
(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com