
科目: 来源: 题型:
【题目】若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A. 抛物线开口向下
B. 抛物线与x轴的交点为(﹣1,0),(3,0)
C. 当x=1时,y有最大值为0
D. 抛物线的对称轴是直线x=![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
科目: 来源: 题型:
【题目】小明和小亮进行摸牌游戏,如图,他们有四张除牌面数字不同外、其他地方完全相同的纸牌,牌面数字分别为4,5,6,7,他们把纸牌背面朝上,充分洗匀后,从这四张纸牌中摸出一张,记下数字放回后,再次重新洗匀,然后再摸出一张,再次记下数字,将两次数字之和做为对比结果.若两次数字之和大于11,则小明胜;若两次数字之和小于11,则小亮胜.
(1)请你用列表法或树状图列出这个摸牌游戏中所有可能出现的结果.
(2)这个游戏公平吗?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】“停课不停学,学习不延期”,某市通过教育资源公共服务平台和有线电视为全市中小学开设在线“空中课堂”,为了解学生每天的学习时间情况,在全市随机抽取了部分初中学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题:
组别 | 学习时间x(h) | 人数(人) |
A | 2.5<x≤3 | 40 |
B | 3<x≤3.5 | 170 |
C | 3.5<x≤4 | 350 |
D | 4<x≤4.5 | |
E | 4.5<x≤5 | 90 |
F | 5小时以上 | 50 |
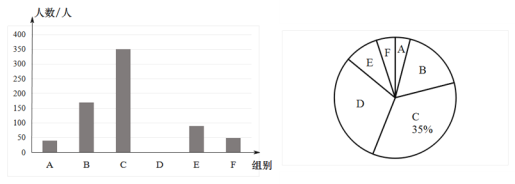
(1)这次参与问卷调查的初中学生有 人,中位数落在 组.
(2)补全条形统计图.
(3)若此市有初中学生2.8万人,求每天参与“空中课堂”学习时间3.5到4.5小时(不包括3.5小时)的初中学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
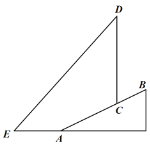
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
查看答案和解析>>
科目: 来源: 题型:
【题目】某市地铁1号线全长约60km,市政府通过招标,甲、乙两家地铁工程公司承担了施工任务,根据招标合同可知,甲公司每月计划施工效率是乙公司的1.2倍,则乙公司单独施工比甲公司单独施工多用10个月,且市政府需要支付给甲公司的施工费用为6亿元/km,乙公司的施工费用为5亿元/km.
(1)甲、乙两家地铁工程公司每月计划施工各为多少km?
(2)由于设备和施工现场只能供一家地铁工程公司单独施工的原因,现计划甲、乙两家公司共用55个月恰好完成施工任务(每家公司施工时间不足一个月按照一个整月计算),且甲公司施工时间不得少于乙公司的两倍,应如何安排才能使市政府支付给两家地铁工程公司的总费用最少?
查看答案和解析>>
科目: 来源: 题型:
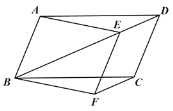
【题目】如图,在□ABCD中,点E是对角线BD上的一点,过点C作CF∥BD,且CF=DE,连接AE、BF、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BFC-∠ABE=90°,判断四边形ABFE的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场销售某种型号防护面罩,进货价为40元/个.经市场销售发现:售价为50元/个时,每周可以售出100个,若每涨价1元,就会少售出5个.供货厂家规定市场售价不得低于50元/个,且商场每周销售数量不得少于80个.
(1)确定商场每周销售这种型号防护面罩所得的利润w(元)与售价x(元/个)之间的函数关系式.
(2)当售价x(元/个)定为多少时,商场每周销售这种防护面罩所得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
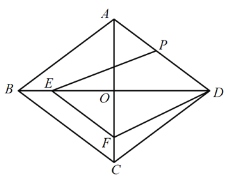
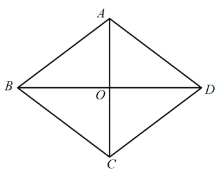
【题目】如图,已知菱形ABCD中,对角线AC、BD相交于点O,且AC=12cm,BD=16cm,点P从点D出发,沿DA方向匀速向点A运动,速度为2cm/s;同时,点E从点B出发,沿BO方向匀速向点O运动,速度为1cm/s,EF∥BC,交OC于点F.当点P、E中有一点停止运动时,另一点也停止运动,线段EF也停止运动,连接PE、DF(0<t<5).解答下列问题:
(1)当t为何值时,PE∥AB?
(2)设四边形EFDP的面积为y(![]() ),求y与t之间的函数关系式.
),求y与t之间的函数关系式.
(3)是否存在某一时刻t,使得![]() ?若存在,求出t的值;若不存在,请说明理由.
?若存在,求出t的值;若不存在,请说明理由.
(4)连接FP,是否存在某一时刻t,使得FP⊥AD?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
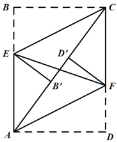
【题目】如图,在矩形ABCD中,点E、F分别在AB、CD边上,AD=6,AB=8,将△CBE沿CE翻折,使B点的对应点B′刚好落在对角线AC上,将△ADF沿AF翻折,使D点的对应点D′也恰好落在对角线AC上,连接EF,则EF的长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com