
科目: 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 上一动点,以
上一动点,以![]() 为边,在
为边,在![]() 的右侧作等边
的右侧作等边![]() .
.
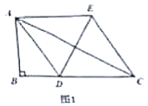

(1)当![]() 平分
平分![]() 时,如图1,四边形
时,如图1,四边形![]() 是________形;
是________形;
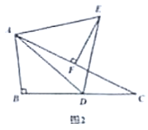
(2)过![]() 作
作![]() 于
于![]() ,如图2,求证:
,如图2,求证:![]() 为
为![]() 的中点;
的中点;
(3)若![]() .
.
①当![]() 为
为![]() 的中点时,过点
的中点时,过点![]() 作
作![]() 于
于![]() ,如图3,求
,如图3,求![]() 的长;
的长;
②点![]() 从
从![]() 点运动到
点运动到![]() 点,则点
点,则点![]() 所经过路径长为________(直接写出结果).
所经过路径长为________(直接写出结果).
查看答案和解析>>
科目: 来源: 题型:
【题目】数学活动课上,小明同学根据学习函数的经验,对函数的图像、性质进行了探究,下面是小明同学探究过程,请补充完整:
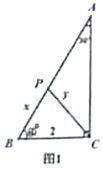
如图1,已知在![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() .设
.设![]() ,
,![]() .
.
(初步感知)
(1)当![]() 时,则①
时,则①![]() ________,②
________,②![]() ________;
________;
(深入思考)
(2)试求![]() 与
与![]() 之间的函数关系式并写出自变量
之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)通过取点测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | _____ | 2 | 2.3 | 2.6 | 3.0 | _____ |
(说明:补全表格时相关数值保留一位小数)
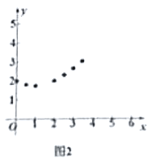
1)建立平面直角坐标系,如图2,描出已补全后的表中各对应值为坐标的点,画出该函数的图象;
2)结合画出的函数图象,写出该函数的两条性质:
①________________________________;②________________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了增强学生的疫情防控意识,响应“停课不停学”号召,某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校2500名学生都参加的网上测试.阅卷后,教务处随机抽取了100份答卷进行分析统计,发现考试成绩(![]() 分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
分数段(分) | 频数(人) | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
合计 | 100 | 1 |

(1)填空:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)将频数分布直方图补充完整;
(3)该校对成绩为![]() 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为
的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为![]() ,请你估算全校获得二等奖的学生人数;
,请你估算全校获得二等奖的学生人数;
(4)结合调查的情况,为了提高疫情防控意识,请你给学校提一条合理性建议.
查看答案和解析>>
科目: 来源: 题型:
【题目】《小猪佩奇》这部动画片,估计同学们都非常喜欢.周末,小猪佩奇一家4口人(小猪佩奇,小猪乔治,小猪妈妈,小猪爸爸)到一家餐厅就餐,包厢有一圆桌,旁边有四个座位(![]() ,
,![]() ,
,![]() ,
,![]() ).
).


(1)小猪佩奇随机坐到![]() 座位的概率是________;
座位的概率是________;
(2)若现在由小猪佩奇,小猪乔治两人先后选座位,用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小明设计的“已知两线段及一角作三角形”的尺规作图过程.
已知:线段![]() ,
,![]() 及∠O .
及∠O .

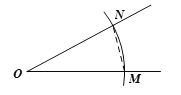
求作:△ABC,使得线段![]() ,
,![]() 及∠O分别是它的两边和一角.
及∠O分别是它的两边和一角.
作法:如图,
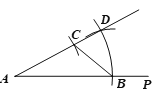
①以点O为圆心,![]() 长为半径画弧,分别交∠O的两边于点M ,N;
长为半径画弧,分别交∠O的两边于点M ,N;
②画一条射线AP,以点A为圆心,![]() 长为半径画弧,交AP于点B;
长为半径画弧,交AP于点B;
③以点B为圆心,MN长为半径画弧,与第②步中所画的弧相交于点D;
④画射线AD;
⑤以点A为圆心,![]() 长为半径画弧,交AD于点C;
长为半径画弧,交AD于点C;
⑥连接BC ,则△ABC即为所求作的三角形.
请回答:
(1)步骤③得到两条线段相等,即 = ;
(2)∠A=∠O的作图依据是 ;
(3)小红说小明的作图不全面,原因是 .
查看答案和解析>>
科目: 来源: 题型:
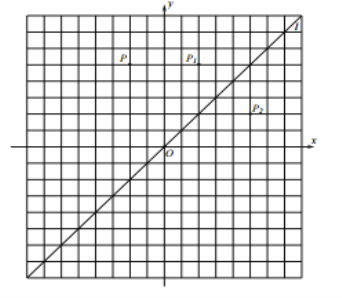
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 为一、三象限角平分线,点
为一、三象限角平分线,点![]() 关于
关于![]() 轴的对称点称为
轴的对称点称为![]() 的一次反射点,记作
的一次反射点,记作![]() ;
;![]() 关于直线
关于直线![]() 的对称点称为点
的对称点称为点![]() 的二次反射点,记作
的二次反射点,记作![]() .
.
例如,点![]() 的一次反射点为
的一次反射点为![]() ,二次反射点为
,二次反射点为![]() .
.
根据定义,回答下列问题:
(1)点![]() 的一次反射点为__________,二次反射点为____________;
的一次反射点为__________,二次反射点为____________;
(2)当点![]() 在第一象限时,点
在第一象限时,点![]() ,
,![]() ,
,![]() 中可以是点
中可以是点![]() 的二次反射点的是___________;
的二次反射点的是___________;
(3)若点![]() 在第二象限,点
在第二象限,点![]() ,
,![]() 分别是点
分别是点![]() 的一次、二次反射点,
的一次、二次反射点,![]() 为等边三角形,求射线
为等边三角形,求射线![]() 与
与![]() 轴所夹锐角的度数.
轴所夹锐角的度数.
(4)若点![]() 在
在![]() 轴左侧,点
轴左侧,点![]() ,
,![]() 分别是点
分别是点![]() 的一次、二次反射点,
的一次、二次反射点,![]() 是等腰直角三角形,请直接写出点
是等腰直角三角形,请直接写出点![]() 在平面直角坐标系
在平面直角坐标系![]() 中的位置.
中的位置.
查看答案和解析>>
科目: 来源: 题型:
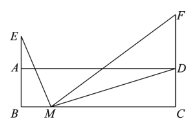
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点D是边BC上的动点,连接AD,点C关于直线AD的对称点为点E,射线BE与射线AD交于点F.


(1)在图1中,依题意补全图形;
(2)记![]() (
(![]() ),求
),求![]() 的大小;(用含
的大小;(用含![]() 的式子表示)
的式子表示)
(3)若△ACE是等边三角形,猜想EF和BC的数量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (
(![]() ).
).
(1)写出抛物线顶点的纵坐标 (用含a的代数式表示);
(2)若该抛物线与x轴的两个交点分别为点A和点B,且点A在点B的左侧,AB=4.
①求a的值;
②记二次函数图象在点A,B之间的部分为W(含点A和点B),若直线![]() (
(![]() )经过(1,-1),且与图形W有公共点,结合函数图象,求b的取值范围.
)经过(1,-1),且与图形W有公共点,结合函数图象,求b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 延长线上的定点,
延长线上的定点,![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
小东根据学习函数的经验,对线段![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小东探究的过程,请补充完整:
(1)对于点![]() 在
在![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
| 0.00 | 0.53 | 1.00 | 1.69 | 2.17 | 2.96 | 3.46 | 3.79 | 4.00 |
| 0.00 | 1.00 | 1.74 | 2.49 | 2.69 | 2.21 | 1.14 | 0.00 | 1.00 |
| 4.12 | 3.61 | 3.16 | 2.52 | 2.09 | 1.44 | 1.14 | 1.02 | 1.00 |
在![]() 的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的两个函数的图象;
中,画出(1)中所确定的两个函数的图象;
(3)结合画出的函数图象,解决问题:当![]() 时,
时,![]() 的长度约为________
的长度约为________![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】某同学模仿二维码的方式为学校设计了一个身份识别图案系统:在![]() 的正方形网格中,黑色正方形表示数字1,白色正方形表示数字0.如图1是某个学生的身份识别图案.约定如下:把第i行,第j列表示的数字记为
的正方形网格中,黑色正方形表示数字1,白色正方形表示数字0.如图1是某个学生的身份识别图案.约定如下:把第i行,第j列表示的数字记为![]() (其中i,j=1,2,3,4),如图1中第2行第1列的数字
(其中i,j=1,2,3,4),如图1中第2行第1列的数字![]() =0;对第i行使用公式
=0;对第i行使用公式![]() 进行计算,所得结果
进行计算,所得结果![]() 表示所在年级,
表示所在年级,![]() 表示所在班级,
表示所在班级,![]() 表示学号的十位数字,
表示学号的十位数字,![]() 表示学号的个位数字.如图1中,第二行
表示学号的个位数字.如图1中,第二行![]() ,说明这个学生在5班.
,说明这个学生在5班.
(1)图1代表的学生所在年级是______年级,他的学号是_________;
(2)请仿照图1,在图2中画出八年级4班学号是36的同学的身份识别图案

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com