
科目: 来源: 题型:
【题目】如图,D、E分别是△ABC的边AB、AC的中点,H、G是边BC上的点,且HG=![]() BC,S△ABC =12,则图中阴影部分的面积为( )
BC,S△ABC =12,则图中阴影部分的面积为( )
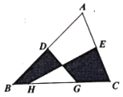
A.6B.4C.3D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.
(1)求抛物线的函数表达式;
(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;
(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,△ABC内接于![]() ,点D是
,点D是![]() 的中点,且与点C位于AB的异侧,CD交AB于点E.
的中点,且与点C位于AB的异侧,CD交AB于点E.
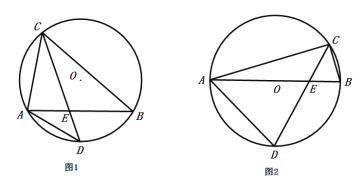
(1)求证:△ADE∽△CDA
(2)如图2,若![]() 的直径AB
的直径AB![]() ,CE=2,求AD和CD的长.
,CE=2,求AD和CD的长.
查看答案和解析>>
科目: 来源: 题型:
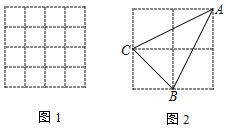
【题目】如图1,每个小正方形的边长都为1,点A、B、C在正方形网格的格点上,AB=5,AC=2,BC=![]() .
.
(1)请在网格中画出△ABC
(2)如图2,直接写出:
①AC= ,BC= .
②△ABC的面积为 .
③AB边上的高为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】科技发展,社会进步,中国已进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗,青少年时期是良好品格形成和知识积累的黄金时期,为此,大数据平台针对部分中学生品格表现和学习状况进行调查统计绘制如下统计图表,请根据图中提供的信息解决下列问题,类别:![]() 品格健全,成绩优异;
品格健全,成绩优异;![]() 尊敬师长,积极进取;
尊敬师长,积极进取;![]() 自控力差,被动学习;
自控力差,被动学习;![]() 沉迷奢玩,消极自卑.
沉迷奢玩,消极自卑.
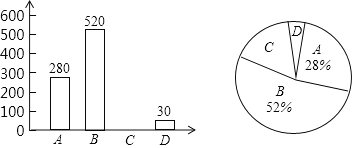
(1)本次调查被抽取的样本容量为 ;
(2)“自控力差,被动学习”的同学有 人,并补全条形统计图;
(3)样本中![]() 类所在扇形的圆心角为 度;
类所在扇形的圆心角为 度;
(4)东至县城内某中学有在校学生3330人,请估算该校![]() 类学生人数.
类学生人数.
查看答案和解析>>
科目: 来源: 题型:
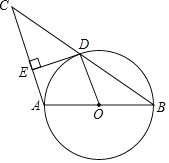
【题目】如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=BC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是_____.
查看答案和解析>>
科目: 来源: 题型:
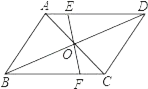
【题目】如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y![]() (k>0,x>0)的图象经过AC的中点D,则k的值为( )
(k>0,x>0)的图象经过AC的中点D,则k的值为( )

A.4B.5C.6D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com