
科目: 来源: 题型:
【题目】近几年,随着电子产品的广泛应用,学生的近视发生率出现低龄化趋势,引起了相关部门的重视.某区为了了解在校学生的近视低龄化情况,对本区7-18岁在校近视学生进行了简单的随机抽样调查,并绘制了以下两幅不完整的统计图.

请根据图中信息,回答下列问题:
(1)这次抽样调查中共调查了近视学生 人;
(2)请补全条形统计图;
(3)扇形统计图中10-12岁部分的圆心角的度数是 ;
(4)据统计,该区7-18岁在校学生近视人数约为10万,请估计其中7-12岁的近视学生人数.
查看答案和解析>>
科目: 来源: 题型:
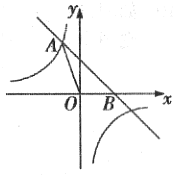
【题目】如图,直线y=﹣x+2与反比例函数y=![]() 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
(1)求该反比例函数的表达式;
(2)写出直线y=﹣x+2向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标
查看答案和解析>>
科目: 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;
(2)用列表法或画树状图法求小丽投放的两袋垃圾是不同类的概率

查看答案和解析>>
科目: 来源: 题型:
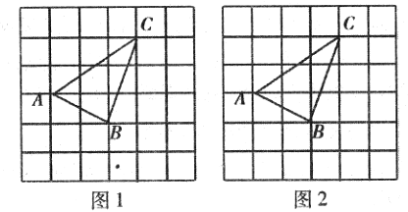
【题目】如图,是由6![]() 6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
(1)在图1中找一个格点D,使以点A、B、C、D为顶点的四边形是平行四边形(画出一种情况即可)
(2)在图2中仅用无刻度的直尺,把线段AB三等分(保留画图痕迹,不写画法)
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC 中,∠A=30°,∠B=90°,AC=8,点 D 在边 AB, 且 BD=![]() ,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019新型冠状病毒,因武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名“2019-nCoV”.冠状病毒是一个大型病毒家族,借助电子显微镜,我们可以看到这些病毒直径约为125纳米(1纳米=1 ![]() 10-9米),125纳米用科学记数法表示等于( )米
10-9米),125纳米用科学记数法表示等于( )米
A.1.25![]() 10-10B.1.25
10-10B.1.25![]() 10-11C.1.25
10-11C.1.25 ![]() 10-8D.1.25
10-8D.1.25![]() 10-7
10-7
查看答案和解析>>
科目: 来源: 题型:
【题目】若一次函数ymxn与反比例函数y![]() 同时经过点P(x,y)则称二次函数ymx2nxk为一次函数与反比例函数的“共享函数”,称点P为共享点.
同时经过点P(x,y)则称二次函数ymx2nxk为一次函数与反比例函数的“共享函数”,称点P为共享点.
(1)判断y2x1与y![]() 是否存在“共享函数”,如果存在,请求出“共享点”.如果不存在,请说明理由;
是否存在“共享函数”,如果存在,请求出“共享点”.如果不存在,请说明理由;
(2)已知:整数m,n,t满足条件t<n<8m,并且一次函数y=(1+n)x+2m+2与反比例函数y![]() 存在“共享函数”y=(m+t)x2+(10mt)x2020,求m的值.
存在“共享函数”y=(m+t)x2+(10mt)x2020,求m的值.
(3)若一次函数yxm和反比例函数y![]() 在自变量x的值满足mxm6的情况下,其“共享函数”的最小值为3,求其“共享函数”的解析式.
在自变量x的值满足mxm6的情况下,其“共享函数”的最小值为3,求其“共享函数”的解析式.
查看答案和解析>>
科目: 来源: 题型:
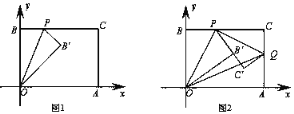
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(1)如图1,当∠BOP=30°时,求点P的坐标;
(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,设AQ=m,试用含有t的式子表示m;
(3)在(2)的条件下,连接OQ,当OQ取得最小值时,求点Q的坐标;
(4)在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
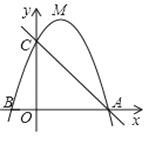
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求抛物线的表达式;
(2)在直线AC的上方的抛物线上,有一点P(不与点M重合),使△ACP的面积等于△ACM的面积,请求出点P的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com