
科目: 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,点
,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() ,
,![]() 两点重合),连接
两点重合),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
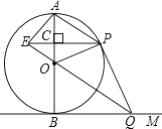
(1)求证:直线![]() 为
为![]() 的切线;
的切线;
(2)若直径![]() 的长为4.
的长为4.
①当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;
②当![]() ________时,四边形
________时,四边形![]() 为菱形.
为菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
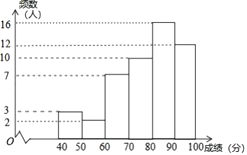
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.
查看答案和解析>>
科目: 来源: 题型:
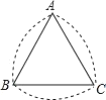
【题目】如图所示的曲边三角形可按下述方法作出:作等边三角形![]() ;分别以点
;分别以点![]() ,
,![]() ,
,![]() 为圆心,以
为圆心,以![]() 的长为半径作
的长为半径作![]() ,
,![]() ,
,![]() .三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为
.三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为![]() ,那么这个曲边三角形的面积是___________.
,那么这个曲边三角形的面积是___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个盒子里装有两个红球,两个白球和一个蓝球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,两次摸到的球的颜色能配成紫色(红色和蓝色能配成紫色)的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
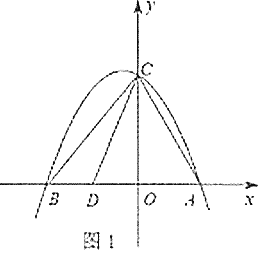
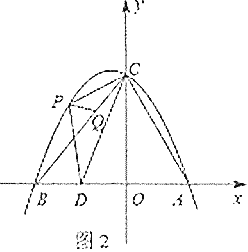
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() ,且点
,且点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() .
.
(1)如图2,点![]() 是直线
是直线![]() 上方抛物线上的一动点,在线段
上方抛物线上的一动点,在线段![]() 上有一动点
上有一动点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的最小值;
的最小值;
(2)将过点![]() 的直线
的直线![]() 绕点
绕点![]() 旋转,设旋转中的直线
旋转,设旋转中的直线![]() 分别与直线
分别与直线![]() 、直线
、直线![]() 交于点
交于点![]() 、
、![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并用相关的思想方法解决问题.
例:若多项式![]() 分解因式的结果中有因式
分解因式的结果中有因式![]() ,求实数
,求实数![]() 的值.
的值.
解:设![]()
若![]() ,则
,则![]() 或
或![]()
由![]() 得
得![]()
则![]() 是方程
是方程![]() 的解
的解
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
解决问题:(1)若多项式![]() 分解因式的结果中有因式
分解因式的结果中有因式![]() ,求实数
,求实数![]() 的值;
的值;
(2)若多项式![]() 分解因式的结果中有因式
分解因式的结果中有因式![]() 和
和![]() .
.
①求出![]() 、
、![]() 的值;
的值;
②直接写出方程![]() 的解.
的解.
查看答案和解析>>
科目: 来源: 题型:
【题目】暑假旅游旺季即将到来,外出旅游的人数不断攀升,去海边游玩是大多数人不错的选择,去海边游玩的人都会选择自己购买海产品进行加工,某商家7月1日进购了一批扇贝与爬爬虾共计200千克,已知扇贝进价10元/千克,售价30元/千克,爬爬虾进价20元/千克,售价30元/千克.
(1)若这批海产品全部售完获利不低于3000元,则扇贝至少进购多少千克?
(2)第一批扇贝和爬爬虾很快售完,于是商家决定购进第二批扇贝与爬爬虾,两种海产品的进价不变,扇贝售价比第一批上涨![]() ,爬爬虾售价比第一批上涨
,爬爬虾售价比第一批上涨![]() ,销量与(1)中获得最低利润时的销量相比,扇贝的销量下降了
,销量与(1)中获得最低利润时的销量相比,扇贝的销量下降了![]() ,爬爬虾的销量不变,结果第二批已经卖掉的扇贝与爬爬虾的销售总额比(1)中第一批扇贝与爬爬虾售完后对应的最低销售总额增加了
,爬爬虾的销量不变,结果第二批已经卖掉的扇贝与爬爬虾的销售总额比(1)中第一批扇贝与爬爬虾售完后对应的最低销售总额增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
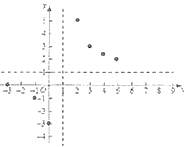
【题目】有这样一个问题:探究函数![]() 的图象与性质,小李根据学习函数的经验,对函数
的图象与性质,小李根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小李探究的过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是______;
的取值范围是______;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
| … |
|
|
| 0 | 2 | 3 | 4 | 5 | … |
| … | 0 |
|
|
| 5 | 3 |
| 2 | … |
则![]() 的值为_______;
的值为_______;
(3)如图所示,在平面直角坐标系![]() 中,根据描出的点,请补全此函数的图象;
中,根据描出的点,请补全此函数的图象;
(4)观察图象,写出该函数的一条性质_______;
(5)若函数![]() 的图象在函数
的图象在函数![]() 的图象上方,直接写出
的图象上方,直接写出![]() 的取值范围_______.
的取值范围_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com