
科目: 来源: 题型:
【题目】重庆是长江上游地区的经济中心、金融中心和创新中心.某公司为了调动员工积极性,将公司员工分成了三个小组进行集分制考核:每月销售业绩第一名集x分,销售业绩第二名集y分,销售业绩第三名集0分(x>y,且均为正整数),经过若干个月(超过4个月)考核后,第一小组集分为23分,第二小组集分为20分,第三小组集分为9分,则第一小组最多得到_____次第二名.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人驾车分别从A、B两地相向而行,乙出发半小时后甲出发,甲出发1.5小时后汽车出现故障,于是甲停下修车,半小时后甲修好后继续沿原路按原速与乙相遇,相遇后甲随即调头以原速返回A地,乙也继续向A地行驶,甲、乙两车之间的距离(y/千米)与甲驾车时间x(小时)之间的关系如图所示,当乙到达A地时,甲距离B地_____千米.
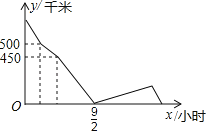
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3![]() ,BC=
,BC=![]() ,点P在BC边上,将△CDP沿DP折叠,点C落在点E处PE、DE分别交AB于点O、F,且OP=OF,则BF的长为_____.
,点P在BC边上,将△CDP沿DP折叠,点C落在点E处PE、DE分别交AB于点O、F,且OP=OF,则BF的长为_____.
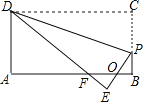
查看答案和解析>>
科目: 来源: 题型:
【题目】现有两组卡片,它们除标号外其他均相同,第一组卡片上分别写有数字“1,2,3”,第二组卡片上分别写有数字“﹣3,﹣1,1,2”,把卡片背面朝上洗匀,先从第一组卡片中随机抽出一张,将其标记为一个点坐标的横坐标,再从第二组卡片中随机抽出一张,将其标记为一个点坐标的纵坐标,则组成的这个点在一次函数y=﹣2x+3上的概率是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A,B(﹣1,0)两点,与y轴交于点C,则下列四个结论:①ac<0;②2a+b=0;③﹣1<x<3时,y<0;④4a+c<0.其中所有正确结论的序号是( )
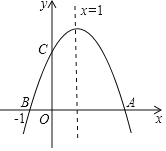
A.①②④B.①③④C.①②③D.②③④
查看答案和解析>>
科目: 来源: 题型:
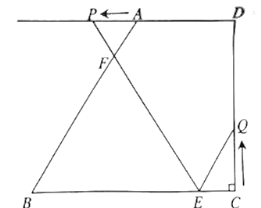
【题目】金佛山是巴蜀四大名山之一游客上金佛山有两种方式:一种是从西坡上山,如图,先从A沿登山步道走到点B,再沿索道乘坐缆车到点C;另一种是从北坡景区沿着盘山公路开车上山到点C.已知在点A处观测点C,得仰角∠CAD=37°,且A、B的水平距离AE=1000米,索道BC的坡度i=1:![]() ,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°=0.75,
,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°=0.75,![]() =1.73)( )
=1.73)( )
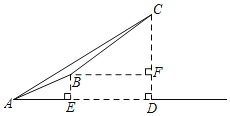
A.2436.8米B.2249.6米C.1036.8米D.1136.8米
查看答案和解析>>
科目: 来源: 题型:
【题目】下列图形都是由大小相同的黑点按一定规律组成的,第①个图形中有3个黑点第②个图形中有11个黑点,第③个图形中有27个黑点,…,按此规律排列,则第⑦个图形中黑点的个数为( )

A.123B.171C.172D.180
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() 同时,点
同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连
,连![]() 接,交
接,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() .解答下列问题:
.解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设五边形![]() 的面积为
的面积为![]() , 求
, 求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)连接![]() .是否存在某一时刻
.是否存在某一时刻![]() , 使点
, 使点![]() 在
在![]() 的垂直平分线上,若存在,求出的值;若不存在,说明理由.
的垂直平分线上,若存在,求出的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?(2×n矩形表示矩形的邻边是2和n)
(探究)不妨假设有an种不同的镶嵌方案.为探究an的变化规律,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:用1个2×1矩形,镶嵌一个2×1矩形,有多少种不同的镶嵌方案?
如图(1),显然只有1种镶嵌方案.所以,a1=1.
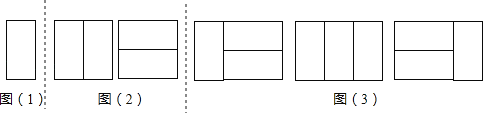
探究二:用2个2×1矩形,镶嵌一个2×2矩形,有多少种不同的镶嵌方案?
如图(2),显然只有2种镶嵌方案.所以,a2=2.
探究三:用3个2×1矩形,镶嵌一个2×3矩形,有多少种不同的镶嵌方案?
一类:在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有1种镶嵌方案;
二类:在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有2种镶嵌方案;
如图(3).所以,a3=1+2=3.
探究四:用4个2×1矩形,镶嵌一个2×4矩形,有多少种不同的镶嵌方案?
一类:在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有 种镶嵌方案;
二类:在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有 种镶嵌方案;
所以,a4= .
探究五:用5个2×1矩形,镶嵌一个2×5矩形,有多少种不同的镶嵌方案?
(仿照上述方法,写出探究过程,不用画图)
……
(结论)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?
(直接写出an与an﹣1,an﹣2的关系式,不写解答过程).
(应用)用10个2×1矩形,镶嵌一个2×10矩形,有 种不同的镶嵌方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com