
科目: 来源: 题型:
【题目】服装店准备购进甲乙两种服装共100件,费用不得超过7500元.甲种服装每件进价80元,每件售价120元;乙种服装每件进价60元,每件售价90元.
(Ⅰ)设购进甲种服装![]() 件,试填写下表.
件,试填写下表.
表一
购进甲种服装的数量/件 | 10 | 20 | … |
|
购进甲种服装所用费用/元 | 800 | 1600 | … | |
购进乙种服装所用费用/元 | 5400 | … |
表二
购进甲种服装的数量/件 | 10 | 20 | … |
|
甲种服装获得的利润/元 | 800 | … | ||
乙种服装获得的利润/元 | 2700 | 2400 | … |
(Ⅱ)给出能够获得最大利润的进货方案,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数、中位数;
(3)请你计算平均数,并估计这260名学生共植树多少棵?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() ,
,![]() 为小正方形边的中点,
为小正方形边的中点,![]() ,
,![]() 为格点,
为格点,![]() 为
为![]() ,
,![]() 的延长线的交点.
的延长线的交点.
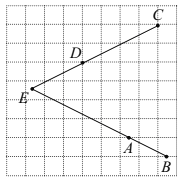
(Ⅰ)![]() 的长等于__________;
的长等于__________;
(Ⅱ)若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,请在如图所示的网格中,用无刻度的直尺,画出线段
,请在如图所示的网格中,用无刻度的直尺,画出线段![]() ,并简要说明点
,并简要说明点![]() ,
,![]() 的位置是如何找到的(不要求证明).
的位置是如何找到的(不要求证明).
____________________________________________________________________.
查看答案和解析>>
科目: 来源: 题型:
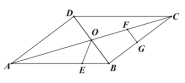
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() 点
点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动时,另一个点也停止运动.连接
;当一个点停止运动时,另一个点也停止运动.连接![]() ,过点
,过点![]() 作
作![]() ,设运动时间为
,设运动时间为![]() ,
,
解答下列问题:
(1)当![]() 为何值时
为何值时![]() 是等腰三角形?
是等腰三角形?
(2)设五边形![]() 面积为
面积为![]() ,试确定
,试确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻![]() 使得
使得![]() 平分
平分![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
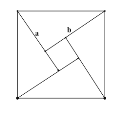
【题目】(问题情境)
我们知道若一个矩形是的周长固定,当相邻两边相等,即为正方形时,它的面积最大.反过来,若一个矩形的面积固定,它的周长是否会有最值呢?
(探究方法)
用两个直角边分别为![]() ,
,![]() 的4个全等的直角三角形可以拼成一个正方形。若
的4个全等的直角三角形可以拼成一个正方形。若![]() ,可以拼成如图所示的正方形,从而得到
,可以拼成如图所示的正方形,从而得到![]() ,即
,即![]() ;当
;当![]() 时,中间小正方形收缩为1个点,此时正方形的面积等于4个直角三角形面积的和.即
时,中间小正方形收缩为1个点,此时正方形的面积等于4个直角三角形面积的和.即![]() .于是我们可以得到结论:
.于是我们可以得到结论:![]() ,
,![]() 为正数,总有
为正数,总有![]() ,当且仅当
,当且仅当![]() 时,代数式
时,代数式![]() 取得最小值
取得最小值![]() .另外,我们也可以通过代数式运算得到类似上面的结论:
.另外,我们也可以通过代数式运算得到类似上面的结论:
∵![]() ,∴
,∴![]() ,
,![]()
∴对于任意实数![]() ,
,![]() 总有
总有![]() ,且当
,且当![]() 时,代数式
时,代数式![]() 取最小值
取最小值![]() .
.
使得上面的方法,对于正数![]() ,
,![]() ,试比较
,试比较![]() 和
和![]() 的大小关系.
的大小关系.
(类比应用)
利用上面所得到的结论完成填空
(1)当![]() 时,代数式
时,代数式![]() 有最 值为 .
有最 值为 .
(2)当![]() 时,代数式
时,代数式![]() 有最 值为 .
有最 值为 .
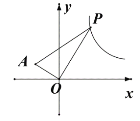
(3)如图,已知![]() 是反比例函数
是反比例函数![]() 图象上任意一动点,
图象上任意一动点,![]() ,
,![]() ,试求
,试求![]() 的最小面积.
的最小面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某服装公司试销一种成本为每件50元的![]() 恤衫.试销中发现,当销售单价是60元时,售出400件;销售单价每降低1元,多售出10件.设试销中销售单价
恤衫.试销中发现,当销售单价是60元时,售出400件;销售单价每降低1元,多售出10件.设试销中销售单价![]() (元)时的销售量为
(元)时的销售量为![]() (件).
(件).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)设该公司获得的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若要销量不低于200件,且获利至少5250元,则售价应在何范围内?
查看答案和解析>>
科目: 来源: 题型:
【题目】为推进生态文明建设,甲、乙两工程队同时为崂山区的两条绿化带铺设草坪.两队所铺设草坪的面积![]() (米)与施工时间
(米)与施工时间![]() (时)之间关系的近似可以用此图象描述.请结合图象解答下列问题:
(时)之间关系的近似可以用此图象描述.请结合图象解答下列问题:
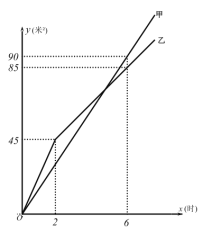
(1)从工作2小时开始,施工方从乙队抽调两人对草坪进行灌溉,乙队速度有所降低,求乙队在工作2小时后![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求乙队降速后,何时铺设草坪面积为甲队的![]() ?
?
(3)乙队降速后,甲乙两队铺设草坪速度之比为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某斜拉桥引申出的部分平面图,AE,CD是两条拉索,其中拉索CD与水平桥面BE的夹角为72°,其底端与立柱AB底端的距离BD为4米,两条拉索顶端距离AC为2米,若要使拉索AE与水平桥面的夹角为35°,请计算拉索AE的长.(结果精确到0.1米)(参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() ,sin72°≈
,sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°≈
,tan72°≈![]() )
)

查看答案和解析>>
科目: 来源: 题型:
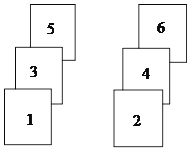
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com