
科目: 来源: 题型:
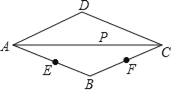
【题目】如图,四边形ABCD是菱形.AB=5,点P是对角线AC上任意一点,E、F分别是AB、BC边上的中点.当点P在线段AC上移动时,则PE+PF的最小值是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),与
点的左侧),与![]() 轴相交于
轴相交于![]() 点,且
点,且![]() .
.
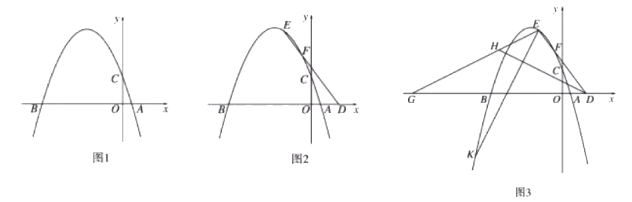
(1)求这条抛物线的解析式;
(2)如图2,![]() 点在
点在![]() 轴上,且在
轴上,且在![]() 点的右侧,
点的右侧,![]() 点为抛物线上第二象限内的点,连接
点为抛物线上第二象限内的点,连接![]() 交抛物线于第二象限内的另外一点
交抛物线于第二象限内的另外一点![]() ,点
,点![]() 到
到![]() 轴的距离与点
轴的距离与点![]() 到
到![]() 轴的距离之比为
轴的距离之比为![]() ,已知
,已知![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图3,在(2)的条件下,点![]() 由
由![]() 出发,沿
出发,沿![]() 轴负方向运动,连接
轴负方向运动,连接![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 中,弦
中,弦![]() 弦
弦![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,![]() .
.
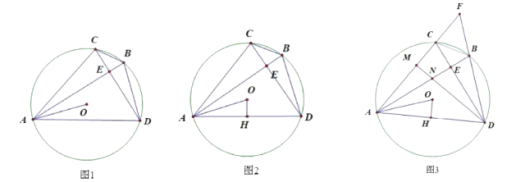
(1)求证:![]()
(2)如图2,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,求证:
,求证:![]()
(3)如图3,在(2)的条件下,延长![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】美丽的雪花扮靓了我们可爱的家乡,但高速公路清雪刻不容缓.某高速公路维护站引进甲、乙两种型号的清雪车,已知甲型清雪车比乙型清雪车每天多清理路段6千米,甲型清雪车清理90千米与乙型清雪车清理60千米路段所用的时间相同.
(1)甲型、乙型清雪车每天各清理路段多少千米?
(2)此公路维护站欲购置甲、乙两种型号清雪车共20台,甲型每台30万元,乙型每台15万元,若在购款不超过360万元,甲型、乙型都购买的情况下,甲型清雪车最多可购买几台?
查看答案和解析>>
科目: 来源: 题型:
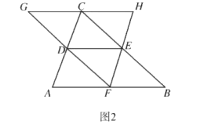
【题目】将等腰三角形![]() 折叠,使顶点
折叠,使顶点![]() 与底边
与底边![]() 的中点
的中点![]() 重合,折线分别交
重合,折线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.
(1)如图1,求证:四边形![]() 是菱形;
是菱形;
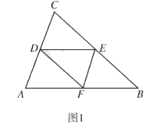
(2)如图2,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,并延长
,并延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在不添加任何辅助线的情况下,请直接写出图2中的所有平行四边形(不包括以
,在不添加任何辅助线的情况下,请直接写出图2中的所有平行四边形(不包括以![]() 为一边的平行四边形)
为一边的平行四边形)
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
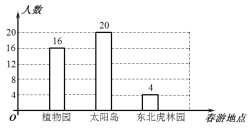
(1)求a的值.
(2)求a名学生中选择去植物园春游的人数占所抽取人数的百分比是多少?
(3)如果该校八年级有440名学生,请你估计选择去太阳岛春游的学生有多少名?
查看答案和解析>>
科目: 来源: 题型:
【题目】图1、图2均是![]() 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点
的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上.在图1、图2中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
均在格点上.在图1、图2中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
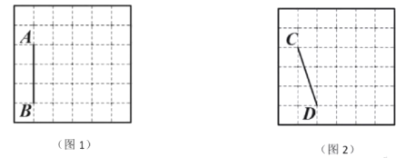
(1)在图1中以线段![]() 为边画一个
为边画一个![]() ,使
,使![]() ,且
,且![]() 的面积为3;
的面积为3;
(2)在图2中以线段![]() 为边画一个四边形
为边画一个四边形![]() ,使四边形
,使四边形![]() 既是轴对称图形又是中心对称图形;
既是轴对称图形又是中心对称图形;
(3)直接写出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 在平面直角坐标系中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.
在平面直角坐标系中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.

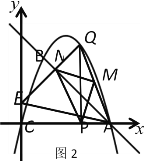

(1)该抛物线的解析式为;
(2)如图1,Q为抛物线上位于直线AB上方的一动点(不与B、A重合),过Q作QP⊥x轴,交x轴于P,连接AQ,M为AQ中点,连接PM,过M作MN⊥PM交直线AB于N,若点P的横坐标为t,点N的横坐标为n,求n与t的函数关系式;在此条件下,如图2,连接QN并延长,交y轴于E,连接AE,求t为何值时,MN∥AE.
(3)如图3,将直线AB绕点A顺时针旋转15度交抛物线对称轴于点C,点T为线段OA上的一动点(不与O、A重合),以点O为圆心、以OT为半径的圆弧与线段OC交于点D,以点A为圆心、以AT为半径的圆弧与线段AC交于点F,连接DF.在点T运动的过程中,四边形ODFA的面积有最大值还是有最小值?请求出该值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com