
科目: 来源: 题型:
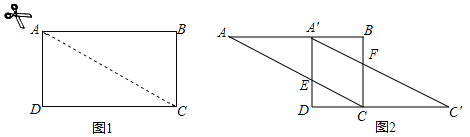
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,沿对角线
,沿对角线![]() 剪开,再把
剪开,再把![]() 沿
沿![]() 方向平移,得到图2,其中
方向平移,得到图2,其中![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)在图2中,除![]() 与
与![]() 外,指出还有哪几对全等三角形(不能添加辅助线和字母),并选择一对加以证明;
外,指出还有哪几对全等三角形(不能添加辅助线和字母),并选择一对加以证明;
(2)设![]() .①当
.①当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形?②设四边形
是菱形?②设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校学生食堂共有座位![]() 个,某天午餐时,食堂中学生人数
个,某天午餐时,食堂中学生人数![]() (人)与时间
(人)与时间![]() (分钟)
(分钟)
变化的函数关系图象如图中的折线![]() .
.
(1)试分别求出当![]() 与
与![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)已知该校学生数有![]() 人,考虑到安全因素,学校决定对剩余
人,考虑到安全因素,学校决定对剩余![]() 名同学延时用餐,即等食堂空闲座位不少于
名同学延时用餐,即等食堂空闲座位不少于![]() 个时,再通知剩余
个时,再通知剩余![]() 名同学用餐.请结合图象分析,这
名同学用餐.请结合图象分析,这![]() 名学生至少要延时多少分钟?
名学生至少要延时多少分钟?

查看答案和解析>>
科目: 来源: 题型:
【题目】某教育主管部门针对中小学生非统考学科的教学情况进行年终考评,抽取某校八年级部分同学的成绩作为样本,把成绩按![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (及格)、
(及格)、![]() (不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.
(不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.
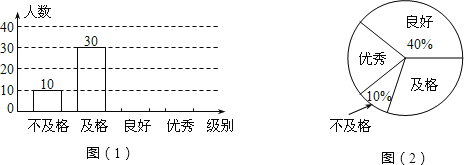
(1)求被抽取的学生人数;
(2)补全条形统计图,并求![]() 的圆心角度数;
的圆心角度数;
(3)该校八年级有![]() 名学生,请估计达到
名学生,请估计达到![]() 、
、![]() 两级的总人数.
两级的总人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是反比例函数![]() 的图象,点
的图象,点![]() ,
,![]() 分别在图象的两支上,以
分别在图象的两支上,以![]() 为对角线作矩形
为对角线作矩形![]() 且
且![]() 轴.
轴.
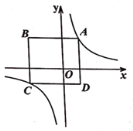
(1)当线段![]() 过原点时,分别写出
过原点时,分别写出![]() 与
与![]() ,
,![]() 与
与![]() 的一个等量关系式;
的一个等量关系式;
(2)当![]() 、
、![]() 两点在直线
两点在直线![]() 上时,求矩形
上时,求矩形![]() 的周长;
的周长;
(3)当![]() 时,探究
时,探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,抛物线![]() 的图象过
的图象过![]() ,
,![]() ,
,![]() 三点,顶点为
三点,顶点为![]() .
.
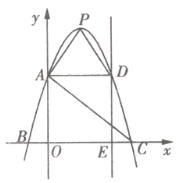
(1)求抛物线的解析式;
(2)设点![]() 在
在![]() 轴上,且
轴上,且![]() ,求
,求![]() 的长;
的长;
(3)若![]() 轴且
轴且![]() 在抛物线上,过
在抛物线上,过![]() 作
作![]() 于
于![]() ,
,![]() 在直线
在直线![]() 上运动,点
上运动,点![]() 在
在![]() 轴上运动,是否存在这样的点
轴上运动,是否存在这样的点![]() 、
、![]() 使以
使以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 、
、![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题引入:如图1所示,正方形![]() 和正方形
和正方形![]() ,则
,则![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() ;
;

(2)类比探究:如图2所示,![]() 为
为![]() 、
、![]() 的中点,正方形
的中点,正方形![]() 和正方形
和正方形![]() 中,判断
中,判断![]() 和
和![]() 的数量关系,并求出
的数量关系,并求出![]() 的值.
的值.
(3)解决问题:
①若把(1)中的正方形都改成矩形,且![]() ,则(1)中的结论还成立吗?若不能成立,请写出
,则(1)中的结论还成立吗?若不能成立,请写出![]() 与
与![]() 的关系,并求出
的关系,并求出![]() 的值;
的值;
②若把(2)中的正方形也都改成矩形,且![]() ,请直接写出
,请直接写出![]() 和
和![]() 的关系以及
的关系以及![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】当今社会人们越来越离不开网络,电脑、手机被普遍使用,与此同时人们的视力也大大受到影响,2019年初某企业以25万元购得某项护目镜生产技术后,再投人100万元购买生产设备,进行该护目镜的生产加工,已知生产这种护目镜的成本价为每件20元,经过市场调研发现该产品的销售单价定在![]() 元比较合理,并且该产品的年销售量
元比较合理,并且该产品的年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的函数关系式为
(元)之间的函数关系式为![]() .(年获利=年销售收入-生产成本-投资成本)
.(年获利=年销售收入-生产成本-投资成本)
(1)求该公司第一年的年获利![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(2)2020年初我国爆发新冠肺炎,该公司决定向红十字会捐款20万元,另外每销售一件产品,就抽出1元钱作为捐款,若除去第一年的最大盈利(或最小亏损)以及第二年的捐款后,到2020年底,两年的总盈利不低于57.5万元,请你确定此时销售单价的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线![]() 表示固定支架,
表示固定支架,![]() 垂直水平桌面
垂直水平桌面![]() ,点
,点![]() 为旋转点,
为旋转点,![]() 可以旋转,当
可以旋转,当![]() 绕点
绕点![]() 逆时针旋转时,投影探头
逆时针旋转时,投影探头![]() 始终垂直于水平桌面
始终垂直于水平桌面![]() ,经测量:
,经测量:![]() ,
,![]() ,
,![]() ,
,![]() .(结果精确到
.(结果精确到![]() )
)

(1)如图2所示,![]() ,
,![]() .
.
①填空:![]() ;
;
②求投影探头的端点![]() 到桌面
到桌面![]() 的距离;
的距离;
(2)如图3所示,将(1)中的![]() 向下旋转,当投影探头的端点
向下旋转,当投影探头的端点![]() 到桌面
到桌面![]() 的距离为
的距离为![]() 时,求
时,求![]() 的大小.(参考数据
的大小.(参考数据![]() span>)
span>)
查看答案和解析>>
科目: 来源: 题型:
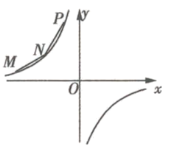
【题目】如图所示,![]() 、
、![]() 、
、![]() 在第二象限,横坐标分别是-4、-2、-1,双曲线
在第二象限,横坐标分别是-4、-2、-1,双曲线![]() 过
过![]() 、
、![]() 、
、![]() 三点,且
三点,且![]() .
.
(1)求双曲线的解析式;
(2)过![]() 点的直线
点的直线![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,且
,且![]() ,且交
,且交![]() 于另一点
于另一点![]() ,求
,求![]() 点坐标;
点坐标;
(3)以![]() 为边(顺时针方向)作正方形
为边(顺时针方向)作正方形![]() ,平移正方形使
,平移正方形使![]() 落在
落在![]() 轴上,点
轴上,点![]() 、
、![]() 对应的点
对应的点![]() 、
、![]() 正好落在反比例函数
正好落在反比例函数![]() 上,求
上,求![]() 对应点
对应点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com