
科目: 来源: 题型:
【题目】若干名工人某天生产同一种玩具,生产的玩具数整理成条形图(如图所示).则他们生产的玩具数的平均数、中位数、众数分别为( )

A.5,5,4 B.5,5,5
C.5,4,5 D.5,4,4
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 时,
时,![]() 点坐标为
点坐标为![]() ;当
;当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,则称点
,则称点![]() 为点
为点![]() 的
的![]() 分变换点(其中
分变换点(其中![]() 为常数).例如:
为常数).例如:![]() 的0分变换点坐标为
的0分变换点坐标为![]() .
.
(1)点![]() 的1分变换点坐标为 ;点
的1分变换点坐标为 ;点![]() 的1分变换点在反比例函数
的1分变换点在反比例函数![]() 图像上,则
图像上,则![]() ;若点
;若点![]() 的1分变换点直线
的1分变换点直线![]() 上,则
上,则![]() ;
;
(2)若点![]() 在二次函数
在二次函数![]() 的图像上,点
的图像上,点![]() 为点
为点![]() 的3分变换点.
的3分变换点.
①直写出点![]() 所在函数的解析式;
所在函数的解析式;
②求点![]() 所在函数的图像与直线
所在函数的图像与直线![]() 交点坐标;
交点坐标;
③当![]() 时,点
时,点![]() 所在函数的函数值
所在函数的函数值![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
(3)点![]() ,
,![]() ,若点
,若点![]() 在二次函数
在二次函数![]() 的图像上,点
的图像上,点![]() 为点
为点![]() 的
的![]() 分变换点.当点
分变换点.当点![]() 所在函数的图像与线段
所在函数的图像与线段![]() 有两个公共点时,直接写出
有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
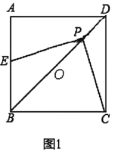
【题目】如图1,在正方形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上任意一点(不与
上任意一点(不与![]() 、
、![]() 重合),点
重合),点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() .
.
初步感知:当点![]() 与点
与点![]() 重合时,比较:
重合时,比较:![]()
![]() (选填“
(选填“![]() ”、“
”、“![]() ”或“
”或“![]() ”).
”).
再次感知:如图1,当点![]() 在线段
在线段![]() 上时,如何判断
上时,如何判断![]() 和
和![]() 数量关系呢?
数量关系呢?
甲同学通过过点![]() 分别向
分别向![]() 和
和![]() 作垂线,构造全等三角形,证明出
作垂线,构造全等三角形,证明出![]() ;
;
乙同学通过连接![]() ,证明出
,证明出![]() ,
,![]() ,从而证明出
,从而证明出![]() .
.
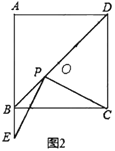
理想感悟:如图2,当点![]() 落在线段
落在线段![]() 上时,判断
上时,判断![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
拓展应用:连接![]() ,并延长
,并延长![]() 交直线
交直线![]() 于点
于点![]() .
.
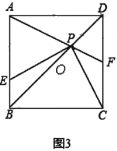
(1)当![]() 时,如图3,直接写出
时,如图3,直接写出![]() 的面积为 ;
的面积为 ;
(2)直接写出![]() 面积
面积![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目: 来源: 题型:
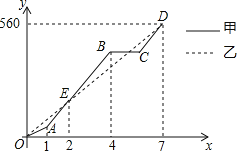
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() ,
,![]() 与时间
与时间![]() 之间的函数关系的图象
之间的函数关系的图象![]() 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题:
![]() 图中E点的坐标是______,题中
图中E点的坐标是______,题中![]() ______
______![]() ,甲在途中休息______h;
,甲在途中休息______h;
![]() 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;
![]() 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
查看答案和解析>>
科目: 来源: 题型:
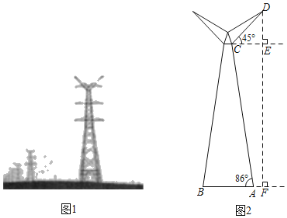
【题目】如图所示,图1,图2分别是某款高压电塔的实物图和示意图电塔的底座AB与地面平齐,DF表示电塔顶端D到地面的距离,已知AF的长是2米,支架AC与地面夹角∠BAC=86°,顶端支架DC长10米,DC与水平线CE之间夹角∠DCE=45°,求电塔的高度DF.(sin86°=0.998,cos86°=0.070,tan86°=14.300,![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
查看答案和解析>>
科目: 来源: 题型:
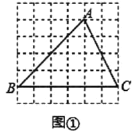
【题目】图①、图②、图③都是![]() 的网格,每个小正方形的顶点称为格点.
的网格,每个小正方形的顶点称为格点.![]() 顶点
顶点![]() 、
、![]() 、
、![]() 均在格点上,在图①、图②、图③给定网格中按要求作图,并保留作图痕迹.
均在格点上,在图①、图②、图③给定网格中按要求作图,并保留作图痕迹.
(1)在图①中画出![]() 中
中![]() 边上的中线
边上的中线![]() ;
;
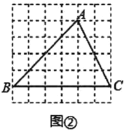
(2)在图②中确定一点![]() ,使得点
,使得点![]() 在
在![]() 边上,且满足
边上,且满足![]() ;
;
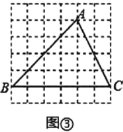
(3)在图③中画出![]() ,使得
,使得![]() 与
与![]() 是位似图形,且点
是位似图形,且点![]() 为位似中心,点
为位似中心,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上,位似比为
边上,位似比为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】由于世界人口增长、水污染以及水资源浪费等原因,全世界面临着淡水资源不足的问题,我国是世界上严重缺水的国家之一.节约用水是水资源合理利用的关键所在,是最快捷、最有效、最可行的维护水资源可持续利用的途径之一,为了调查居民的用水情况,有关部门对某小区的20户居民的月用水量进行了调查,数据如下(单位![]() ):
):
6.7 8.7 7.3 11.4 7.0 6.9 11.7 9.7 10.0 9.7
7.3 8.4 10.6 8.7 7.2 8.7 10.5 9.3 8.4 8.7
整理数据:按如下分段整理样本数据并补充表格(表1):
用水量 |
|
|
|
|
人数 |
| 6 | b | 4 |
分析数据:补全下列表格中的统计量(表2):
平均数 | 中位数 | 众数 |
8.85 |
| 8.7 |
得出结论:
(1)表中的![]() ,
,![]() ,
,![]() ;
;
(2)若用表1中的数据制作一个扇形统计图,![]() 所占的扇形圆心角的度数为 度;
所占的扇形圆心角的度数为 度;
(3)如果该小区有住户400户,根据样本估计用水量在![]() 的居民有多少户?
的居民有多少户?
查看答案和解析>>
科目: 来源: 题型:
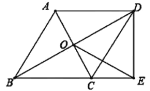
【题目】如图,![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 的平行线与
的平行线与![]() 的平分线交于点
的平分线交于点![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 的延长线交于
的延长线交于![]() 点,连接
点,连接![]() ,若
,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长为 .
的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com