
科目: 来源: 题型:
【题目】在“全国爱眼日”这天,某校课题小组为了了解本校![]() 名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
组别 | 视力 | 频率 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|

根据以上信息解答下列问题:
![]() 填空:
填空:![]() ______ _,并将频数分布直方图补充完整;
______ _,并将频数分布直方图补充完整;
![]() 若将统计结果绘制成扇形统计图,则第
若将统计结果绘制成扇形统计图,则第![]() 组所在扇形的圆心角度数为 ;
组所在扇形的圆心角度数为 ;
![]() 课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
视力 |
|
|
|
|
|
比重 |
|
|
|
|
|
根据调查结果估计该校有多少名学生的视力下降是由于过度使用电子产品.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AC、BD为对角线,AB=2,把BD绕点B逆时针旋转,得到线段BE,当点E落在线段BA的延长线时,恰有DE∥AC,连接CE,则阴影部分的面积为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图①,在等腰直角![]() 中,斜边
中,斜边![]() .
.
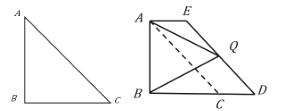
(1)请你在图①的![]() 边上求作一点
边上求作一点![]() ,使得
,使得![]() ;
;
(2)如图②,在(1)问的条件下,将![]() 边沿
边沿![]() 方向平移,使得点
方向平移,使得点![]() 、
、![]() 、
、![]() 对应点分别为
对应点分别为![]() 、
、![]() 、
、![]() ,连接
,连接![]() ,
,![]() .若平移的距离为1,求
.若平移的距离为1,求![]() 的大小及此时四边形
的大小及此时四边形![]() 的面积;
的面积;
(3)将![]() 边沿
边沿![]() 方向平移
方向平移![]() 个单位至
个单位至![]() ,是否存在这样的
,是否存在这样的![]() ,使得在直线
,使得在直线![]() 上有一点
上有一点![]() ,满足
,满足![]() ,且此时四边形
,且此时四边形![]() 的面积最大?若存在,求出四边形
的面积最大?若存在,求出四边形![]() 面积的最大值及平移距离
面积的最大值及平移距离![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
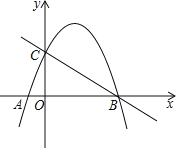
【题目】抛物线![]() 经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
经过点A(-1,0)、B(4,0),与y轴交于点C(0,4).
(1)求抛物线的表达式;
(2)点P为直线BC上方抛物线的一点,分别连接PB、PC,若直线BC恰好平分四边形COBP的面积,求P点坐标;
(3)在(2)的条件下,是否在该抛物线上存在一点Q,该抛物线对称轴上存在一点N,使得以A、P、Q、N为顶点的四边形为平行四边形?若存在,求出Q点坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】篮球运动是全世界最流行的运动之一,近年流行于青少年之间的“3对3”篮球将登上2020年奥运会赛场,为备战某市中学生“3对3”篮球联赛,某校甲、乙、丙三位同学作为“兄弟战队”的主力队员进行篮球传球训练,篮球由一个人随机传给另一个人,且每位传球人传球给其余两人的机会是均等的,现在由甲开始传球.
(1)求甲第一次传球给乙的概率;
(2)三次传球后,篮球在谁手中的可能性大?请利用树状图说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着“西成高铁”的开通,对于加强关中一天水经济区与成渝经济区的交流合作,促进区域经济发展和提高人民出行质量,具有十分重要的意义.成都某单位计划组织优秀员工利用周末乘坐“西成高铁”到西安观光旅游,计划游览著名景点“大唐芙蓉园”,该景区团体票价格设置如下:
人数/人 | 10人以内(含10人) | 超过10人但不超过30人的部分 | 超过30人的部分 |
单价(元/张) | 120 | 108 | 96 |
(1)求团体票价![]() 与游览人数
与游览人数![]() 之间的函数关系式;
之间的函数关系式;
(2)若该单位购买团体票共花费3456元,且所有人都购买了门票,那么该单位共有多少人游览了“大唐芙蓉园”?
查看答案和解析>>
科目: 来源: 题型:
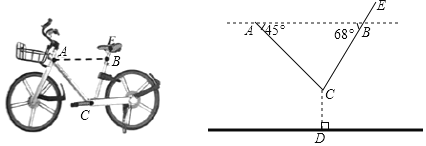
【题目】如图所示,一辆单车放在水平的地面上,车把头下方![]() 处与坐垫下方
处与坐垫下方![]() 处在平行于地面的同一水平线上,
处在平行于地面的同一水平线上,![]() ,
,![]() 之间的距离约为
之间的距离约为![]() ,现测得
,现测得![]() ,
,![]() 与
与![]() 的夹角分别为
的夹角分别为![]() 与
与![]() ,若点
,若点![]() 到地面的距离
到地面的距离![]() 为
为![]() ,坐垫中轴
,坐垫中轴![]() 处与点
处与点![]() 的距离
的距离![]() 为
为![]() ,求点
,求点![]() 到地面的距离(结果保留一位小数).(参考数据:
到地面的距离(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
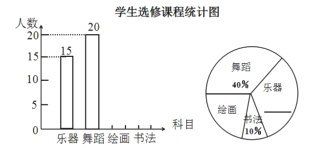
(1)补全条形统计图,补全扇形统计图中乐器所占的百分比;
(2)本次调查学生选修课程的“众数”是__________;
(3)若该校有1200名学生,请估计选修绘画的学生大约有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com