
科目: 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
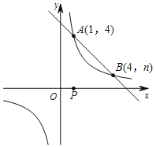
(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目: 来源: 题型:
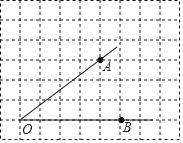
【题目】如图,已知方格纸中的每个小方格都是相同的正方形(边长为1),方格纸上有一个角∠AOB,A,O,B均为格点,请回答问题并只用无刻度直尺和铅笔,完成下列作图并简要说明画法:
(1)OA=_____;
(2)作出∠AOB的平分线并在其上标出一个点Q,使OQ=![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标是(3,0),对称轴为直线x=1,下列结论:①abc>0;②2a+b=0;③4a﹣2b+c>0;④当y>0时,﹣1<x<3;⑤b<c.其中正确的个数是( )
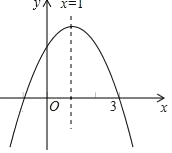
A.2B.3C.4D.5
查看答案和解析>>
科目: 来源: 题型:
【题目】某校申报“跳绳特色运动”学校一年后,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
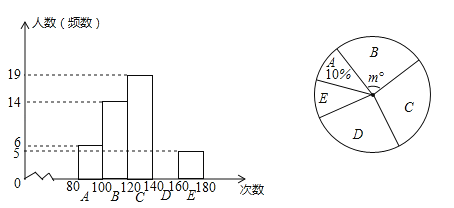
(1)补全频数分布直方图,扇形图中m= ;
(2)若把每组中各个数据用这组数据的中间值代替(如A组80≤x<100的中间值是(![]() =90次),则这次调查的样本平均数是多少;
=90次),则这次调查的样本平均数是多少;
(3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人.
查看答案和解析>>
科目: 来源: 题型:
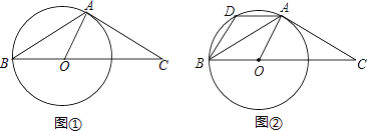
【题目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(1)如图①,若⊙O的半径为5,求线段OC的长;
(2)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
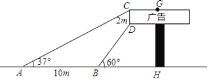
【题目】如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
科目: 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)根据题意,填写下表:
重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
甲公司 | _________ | 22 | _________ | 67 | … |
乙公司 | 11 | ________ | 51 | _________ | … |
(2)请分别写出甲乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(3)小明应选择哪家快递公司更省钱?
查看答案和解析>>
科目: 来源: 题型:
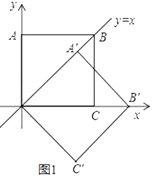
【题目】在平面直角坐标系中,O为原点,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,现将正方形OABC绕点O顺时针旋转.
(1)如图①,当点A的对应的A′落在直线y=x上时,点A′的对应坐标为________;点B的对应点B′的坐标为_________;
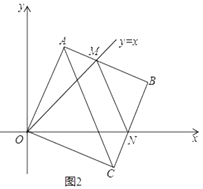
(2)旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N,当A点第一次落在直线y=x上时,停止旋转.
①如图2,在正方形OABC旋转过程中,线段AM,MN,NC三者满足什么样的数量关系?请说明理由;
②当AC∥MN时,求△MBN内切圆的半径(直接写出结果即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=x+3的图象与x轴交于点A,二次函数y=x2+mx+n的图象经过点A.
(1)当m=4时,求n的值;
(2)设m=﹣2,当﹣3≤x≤0时,求二次函数y=x2+mx+n的最小值;
(3)当﹣3≤x≤0时,若二次函数﹣3≤x≤0时的最小值为﹣4,求m、n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com