
科目: 来源: 题型:
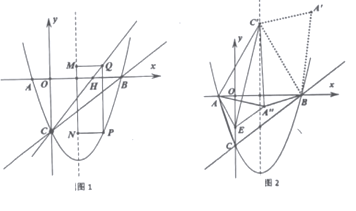
【题目】如图![]() ,在平面直角坐标系中,抛物线
,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,若点
,若点![]() 是第四象限内抛物线上的一个动点,且在对称轴的右侧,过点
是第四象限内抛物线上的一个动点,且在对称轴的右侧,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,作
,作![]() 轴交对称轴于点
轴交对称轴于点![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() ,当矩形
,当矩形![]() 的周长最大时,在
的周长最大时,在![]() 轴上有一动点
轴上有一动点![]() ,
,![]() 轴上有一动点
轴上有一动点![]() ,一动点
,一动点![]() 从线段
从线段![]() 的中点
的中点![]() 出发以每秒
出发以每秒![]() 个单位的速度沿
个单位的速度沿![]() 的路径运动到点
的路径运动到点![]() ,再沿线段
,再沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 点处停止运动,求动点
点处停止运动,求动点![]() 运动时间的最小值:
运动时间的最小值:
(2)如图![]() , 将
, 将![]() 绕点
绕点![]() 顺时针旋转至
顺时针旋转至![]() 的位置, 点
的位置, 点![]() 的对应点分别为
的对应点分别为![]() ,且点
,且点![]() 恰好落在抛物线的对称轴上,连接
恰好落在抛物线的对称轴上,连接![]() .点
.点![]() 是
是![]() 轴上的一个动点,连接
轴上的一个动点,连接![]() , 将
, 将![]() 沿直线
沿直线![]() 翻折为
翻折为![]() , 是否存在点
, 是否存在点![]() , 使得
, 使得![]() 为等腰三角形?若存在,请求出点
为等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们已经知道一些特殊的勾股数,如三连续正整数中的勾股数:3、4、5;三个连续的偶数中的勾股数6、8、10;事实上,勾股数的正整数倍仍然是勾股数.
(1)另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派提出的公式:a=2n+1,b=2n2+2n,c=2n2+2n+1(n为正整数)是一组勾股数,请证明满足以上公式的a、b、c的数是一组勾股数.
(2)然而,世界上第一次给出的勾股数公式,收集在我国古代的着名数学着作《九章算术》中,书中提到:当a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
(m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 与
与![]() 成反比例
成反比例![]() 与
与![]() 成正比例,函数的自变量
成正比例,函数的自变量![]() 的取值范围是
的取值范围是![]() ,且当
,且当![]() 或
或![]() 时,
时,![]() 的值均为
的值均为![]() 。
。
请对该函数及其图象进行如下探究:
(1)解析式探究:根据给定的条件,可以确定出该函数的解析式为: .
(2)函数图象探宄:①根据解析式,选取适当的自变量![]() ,并完成下表:
,并完成下表:
|
| ... | ||||||||
| ... |
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.
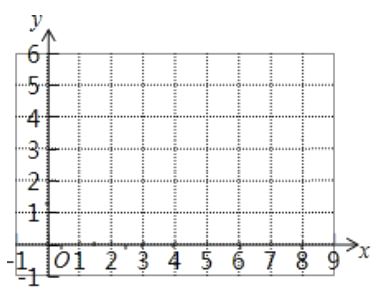
(3)结合画出的函数图象,解决问题:
①当![]() ,
,![]() ,
,![]() 时,函数值分别为
时,函数值分别为![]() ,则
,则![]() 的大小关系为: (用“
的大小关系为: (用“![]() ”或“
”或“![]() ”表示)
”表示)
②若直线![]() 与该函数图象有两个交点,则
与该函数图象有两个交点,则![]() 的取值范围是 ,此时,
的取值范围是 ,此时,![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂家以A、B两种原料,利用不同的工艺手法生产出了甲、乙两种袋装产品,其中,甲产品每袋含1.5千克A原料、1.5千克B原料;乙产品每袋含2千克A原料、1千克B原料.甲、乙两种产品每袋的成本价分别为袋中两种原料的成本价之和.若甲产品每袋售价72元,则利润率为20%.某节庆日,厂家准备生产若干袋甲产品和乙产品,甲产品和乙产品的数量和不超过100袋,会计在核算成本的时候把A原料和B原料的单价看反了,后面发现如果不看反,那么实际成本比核算时的成本少500元,那么厂家在生产甲乙两种产品时实际成本最多为_____元.
查看答案和解析>>
科目: 来源: 题型:
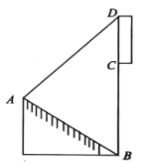
【题目】小明在某个斜坡![]() 上,看到对面某高楼
上,看到对面某高楼![]() 上方有一块宜传“中国国际进口博览会”的竖直标语牌
上方有一块宜传“中国国际进口博览会”的竖直标语牌![]() .小明在
.小明在![]() 点测得标语牌顶端D处的仰角为
点测得标语牌顶端D处的仰角为![]() ,并且测得斜坡
,并且测得斜坡![]() 的坡度为
的坡度为![]() (
(![]() 在同一条直线上),已知斜坡
在同一条直线上),已知斜坡![]() 长
长![]() 米,高楼高
米,高楼高![]() 米(即
米(即![]() 米),则标语牌
米),则标语牌![]() 的长是( )米.(结果保留小数点后一位)(参考数据:
的长是( )米.(结果保留小数点后一位)(参考数据:![]() ,
, ![]() ,
, ![]() ,
,![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() 三个点.
三个点.
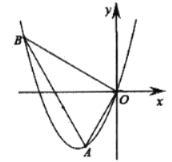
(1)求抛物线解析式;
(2)若点![]() ,
,![]() 为该抛物线上的两点,且
为该抛物线上的两点,且![]() .求
.求![]() 的取值范围;
的取值范围;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() (不与点
(不与点![]() ,点
,点![]() 重合),使点
重合),使点![]() ,点
,点![]() 到直线
到直线![]() 的距离之和最大?若存在,求
的距离之和最大?若存在,求![]() 的度数,并直接写出点
的度数,并直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为![]() ,则新三角形与原三角形相似.
,则新三角形与原三角形相似.
观点二:将邻边为![]() 和
和![]() 的矩形按图2方式向内缩小,得到新的矩形,它们对应的边间距都为
的矩形按图2方式向内缩小,得到新的矩形,它们对应的边间距都为![]() ,则新矩形与原矩形相似.
,则新矩形与原矩形相似.
请回答下列问题:

(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 按图3的方式向外扩张,得到
按图3的方式向外扩张,得到![]() ,它们对应的边间距都为
,它们对应的边间距都为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】合肥百大集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
空调机 | 电冰箱 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,才能使总利润达到最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com