
科目: 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
查看答案和解析>>
科目: 来源: 题型:
【题目】901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:

(1)该班的学生共有 名;
(2)若该班参加“吉他社”与“街舞社”的人数相同,请你计算,“吉他社”对应扇形的圆心角的度数;
(3)901班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )

A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
科目: 来源: 题型:
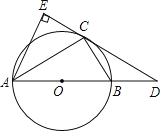
【题目】如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,点D是AB延长线上的一点,AE⊥DC交DC的延长线于点E,AC平分∠DAE.
(1)DE与⊙O有何位置关系?请说明理由.
(2)若AB=6,CD=4,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
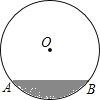
【题目】在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.
(1)若油面宽AB=16dm,求油的最大深度.
(2)在(1)的条件下,若油面宽变为CD=30dm,求油的最大深度上升了多少dm?
查看答案和解析>>
科目: 来源: 题型:
【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
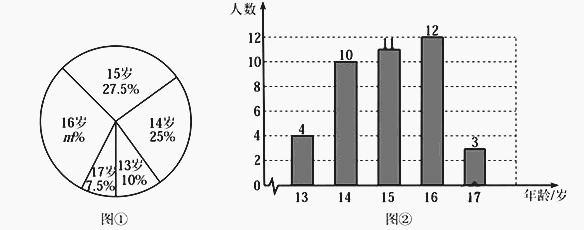
(1)本次接受调查的跳水运动员人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
查看答案和解析>>
科目: 来源: 题型:
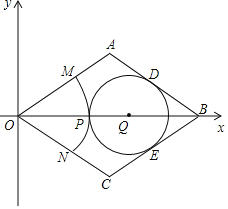
【题目】如图,菱形OABC的顶点O在坐标原点,顶点B在x轴的正半轴上,OA边在直线y=![]() x上,AB边在直线y=-
x上,AB边在直线y=-![]() x+2上.
x+2上.
(1)直接写出:线段OA等于多少,∠AOC等于多少度;
(2)在对角线OB上有一动点P,以O为圆心,OP为半径画弧MN,分别交菱形的边OA、OC于点M、N,作⊙Q与边AB、BC、弧MN都相切,⊙Q分别与边AB、BC相切于点D、E,设⊙Q的半径为r,OP的长为y,求y与r之间的函数关系式,并写出自变量r的取值范围;
(3)若以O为圆心、OA长为半径作扇形OAC,请问在菱形OABC中,在除去扇形OAC后的剩余部分内,是否可以截下一个圆,使得它与扇形OAC刚好围成一个圆锥,若可以,求出这个圆的半径,若不可以,说明理由.
查看答案和解析>>
科目: 来源: 题型:
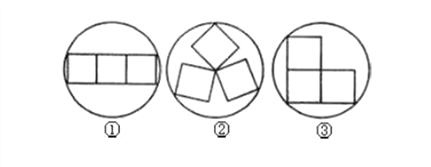
【题目】在一节数学实践活动课上,老师拿出三个边长都为5cm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com