
科目: 来源: 题型:
【题目】如图,菱形ABCD中,∠ABC=60°,E为AB中点,F为BC上一点,GカCD上一点,连接EF,FG,且∠BFE=∠CFG.
(1)若G为CD中点吋,求证:EF=FG;
(2)设![]() ,
,![]() ,求y芙于x的函数解析式.
,求y芙于x的函数解析式.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是某品牌的一款学生斜持包,其挎带由单层部分、双层部分和调节扣组成.设单层部分的长度为xcm,双层部分的长度为ycm,经测景,得到如下数据:
x(cm) | 0 | 4 | 6 | 8 | 10 | … | 120 |
y(cm) | M | 58 | 57 | 56 | 55 | … | n |
(1)如图2,在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用平滑曲线连接,并根据图象猜想求出该函数的解析式;
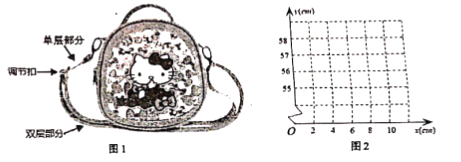
(2)若小花要购买一个持带长为125cm的斜挎包,该款式的斜挎包是否满足小花的需求?请说明理由,(挎带的总长度=单层部分长度+双层部分长度,其中调节扣的长度忽略不计)
查看答案和解析>>
科目: 来源: 题型:
【题目】电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
获得好评的电影部数 | 56 | 10 | 45 | 50 | 160 | 51 |
(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率:
(2)电影公司为增加投资回报,需在调查前根据经验预估每类电影的好评率(好评率是指:一类电影中获得好评的部数与该类电影的部数的比值),如表所示:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
预估好评率 | 0.5 | 0.2 | 0.15 | 0.15 | 0.4 | 0.3 |
定义统计最![]() 其中
其中![]() 为第i类电影的实际好评率,
为第i类电影的实际好评率,![]() 为第i类电影的预估好评率(i=1,2,...,n).规定:若S<0.05,则称该次电影的好评率预估合理,否则为不合理,判断本次电影的好评率预估是否合理。
为第i类电影的预估好评率(i=1,2,...,n).规定:若S<0.05,则称该次电影的好评率预估合理,否则为不合理,判断本次电影的好评率预估是否合理。
查看答案和解析>>
科目: 来源: 题型:
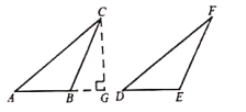
【题目】问题提出学习了全等三角形的判定方法(“SSS”“SAS”“ASA”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
初步思考:将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF.然后对∠ABC进行分类,可分为“∠ABC是锐角、直角、钝角”三种情况进行探究。
第一种情况:当∠ABC是锐角时,AB=DE不一定成立;
第二种情况:当∠ABC是直角时,根据“HL”,可得△ABC≌ΔDEF,则AB=DE;
第三种情况:当∠ADC是钝角时,则AB=DE.
如图,在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,且∠ABC是钝角,求证:AB=DE.
方法归纳化归是一种有效的数学思维方式,一般是将未解决的问题通过交换转化为已解决的问题.观群发现第三种情况可以转化为第二种情况,如图,过点C作CG⊥AB交廷长线于点G.
(1)在ΔDEF中用尺规作出DE边上的高FH,不写作法,保留作图痕迹;
(2)请你完成(1)中作图的基础上,加以证明AB=DE.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O为正方形ABCD对角线上一点,以点O为圆心,OA长为半径的
⊙ O与BC相切于点E.
(1)求证:CD是⊙ O的切线;
(2)若正方形ABCD的边长为10,求⊙O的半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为10的半圆形量角器中,而一个直径为10的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是
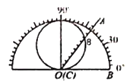
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
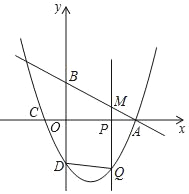
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
(1)求点A的坐标.
(2)求抛物线的表达式.
(3)当以B、D、Q,M为顶点的四边形是平行四边形时,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】某市实施产业精准扶贫,帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克,到了收获季节投入市场销售时,调查市场行情后,发现该蜜柚不会亏本,且每天的销售量y(千克)与销售单价x(元)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某村农户今年共采摘蜜柚12000千克,若该品种蜜柚的保质期为50天,按照(2)的销售方式,能否在保质期内全部销售完这批蜜柚?若能,请说明理由;若不能,应定销售价为多少元时,既能销售完又能获得最大利润?

查看答案和解析>>
科目: 来源: 题型:
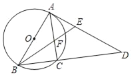
【题目】如图,以AB为直径的⊙O外接于△ABC,点D在BC的延长线上,∠ABC的角平分线与AD交于E点,与AC交于F点,且AE=AF.
(1)证明直线AD是⊙O的切线;
(2)若AD=16,sinD=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com