
科目: 来源: 题型:
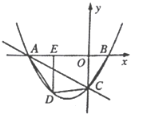
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,经过点
,经过点![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为点
轴的另一个交点为点![]() ,点
,点![]() 是抛物线上一点,过点
是抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当点
当点![]() 在第三象限,设
在第三象限,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
![]() 连接
连接![]() ,若
,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 尝试探究
尝试探究
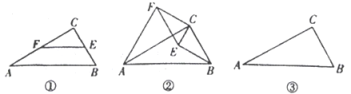
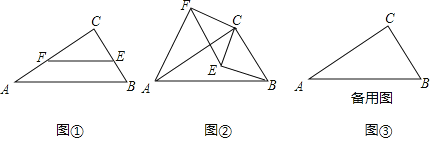
如图-![]() ,在△ABC中,∠C=90°,∠A=30°,点E、F分别是BC、AC边上的点,且EF//BC.
,在△ABC中,∠C=90°,∠A=30°,点E、F分别是BC、AC边上的点,且EF//BC.
![]()
![]() 的值为 ;
的值为 ;![]() 直线
直线![]() 与直线
与直线![]() 的位置关系为 ;
的位置关系为 ;
![]() 类比延伸
类比延伸
如图![]() ,若将图
,若将图![]() 中的
中的![]() 绕点
绕点![]() 顺时针旋转,连接
顺时针旋转,连接![]() ,则在旋转的过程中,请判断
,则在旋转的过程中,请判断![]() 的值及直线
的值及直线![]() 与直
与直![]() 线的位置关系,并说明理由;
线的位置关系,并说明理由;
![]() 拓展运用
拓展运用
若![]() ,在旋转过程中,当
,在旋转过程中,当![]() 三点在同一直线上时,请直接写出此时线段
三点在同一直线上时,请直接写出此时线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种水果进价为每千克15元,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克.设销售单价为![]() (元),每天的销售量为
(元),每天的销售量为![]() (千克),每天获利为
(千克),每天获利为![]() (元).
(元).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 与
与![]() 之间的函数关系式;该水果定价为每千克多少元时,每天的销售利润最大?最大利润是多少元?
之间的函数关系式;该水果定价为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种水果每天的销售量不低于40千克,求商家每天销售利润的最大值是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.
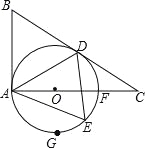
(1)求证:BD是⊙O的切线.
(2)若AB=![]() ,E是半圆
,E是半圆![]() 上一动点,连接AE,AD,DE.
上一动点,连接AE,AD,DE.
填空:
①当![]() 的长度是____________时,四边形ABDE是菱形;
的长度是____________时,四边形ABDE是菱形;
②当![]() 的长度是____________时,△ADE是直角三角形.
的长度是____________时,△ADE是直角三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】每年5月20日是中国学生营养日,按时吃早餐是一种健康的饮食习惯,为了解本校九年级学生饮食习惯,某兴趣小组在九年级随机抽取了一部分学生每天吃早餐的情况,并将统计结果绘制成如下不完整的统计图表:
组别 | 调查结果 | 所占百分比 |
A | 不吃早餐 | 25% |
B | 偶尔吃早餐 | 12.5% |
C | 经常吃早餐 | |
D | 每天吃早餐 | 50% |

请根据以上统计图表,解答下列问题:
![]() 本次接受调查的总人数为_____人.
本次接受调查的总人数为_____人.
![]() 请补全条形统计图.
请补全条形统计图.
![]() 该校九年级共有学生
该校九年级共有学生![]() 人,请估计该校九年级学生每天吃早餐的人数;
人,请估计该校九年级学生每天吃早餐的人数;
![]() 请根据此次调查的结果提一条建议.
请根据此次调查的结果提一条建议.
查看答案和解析>>
科目: 来源: 题型:
【题目】现有四张质地均匀,大小完全相同的卡片,在其正面分别标有数字﹣1,﹣2,2,3,把卡片背面朝上洗匀,从中随机抽出一张后,不放回,再从中随机抽出一张,则两次抽出的卡片所标数字之和为正数的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
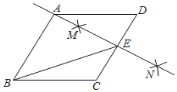
【题目】如图,在菱形![]() 中,
中,![]() ,按以下步骤作图:①分别以点
,按以下步骤作图:①分别以点![]() 和点
和点![]() 为圆心,为圆心,大于号
为圆心,为圆心,大于号![]() 的长为半径面狐,两弧交于点
的长为半径面狐,两弧交于点![]() ,
,![]() :②做直线
:②做直线![]() ,且
,且![]() 恰好经过点
恰好经过点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,经过点
,经过点![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为点
轴的另一个交点为点![]() ,点
,点![]() 是抛物线上一点,过点
是抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
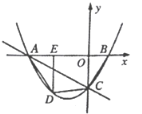
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当点
当点![]() 在第三象限,设
在第三象限,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
![]() 连接
连接![]() ,若
,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)尝试探究
如图①,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() .
.
①![]() 的值为多少;②直线
的值为多少;②直线![]() 与直线
与直线![]() 的位置关系;
的位置关系;
(2)类比延伸
如图②,若将图①中的![]() 绕点
绕点![]() 顺时针旋转,连接
顺时针旋转,连接![]() ,
,![]() ,则在旋转的过程中,请判断
,则在旋转的过程中,请判断![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)拓展运用
若![]() ,
,![]() ,在旋转过程中,当
,在旋转过程中,当![]() ,
,![]() ,
,![]() 三点在同一直线上时,请直接写出此时线段
三点在同一直线上时,请直接写出此时线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种水果进价为每千克15元,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克.设销售单价为![]() (元),每天的销售量为
(元),每天的销售量为![]() (千克),每天获利为
(千克),每天获利为![]() (元).
(元).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 与
与![]() 之间的函数关系式;该水果定价为每千克多少元时,每天的销售利润最大?最大利润是多少元?
之间的函数关系式;该水果定价为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种水果每天的销售量不低于40千克,求商家每天销售利润的最大值是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com