
科目: 来源: 题型:
【题目】如图是一个圆,一只电子跳蚤在标有数字的五个点上跳跃.若它停在奇数点上时,则一次沿顺时针方向跳两个点;若停在偶数点上时,则下一次沿逆时针方向跳一个点.若这只跳蚤从1这点开始跳,则经过2019次跳后它所停在的点对应的数为( )
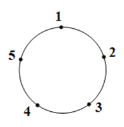
A. 1 B. 2 C. 4 D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在边BC和DC上,连接AE、BF,AE⊥BF,点M、N分别在边AB、DC上,连接MN,若MN∥BC,FN=1,BE=2,则BM=_____.
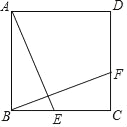
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.
(1)求证:四边形ABEF是菱形;(2)若BC=8,∠ABC=60°,求OC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
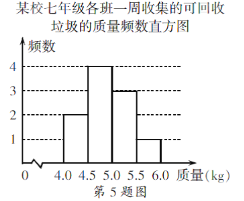
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
查看答案和解析>>
科目: 来源: 题型:
【题目】知识背景
当a>0且x>0时,因为(![]() ﹣
﹣![]() )2≥0,所以x﹣2
)2≥0,所以x﹣2![]() +
+![]() ≥0,从而x+
≥0,从而x+![]() (当x=
(当x=![]() 时取等号).
时取等号).
设函数y=x+![]() (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=![]() 时,该函数有最小值为2
时,该函数有最小值为2![]() .
.
应用举例
已知函数为y1=x(x>0)与函数y2=![]() (x>0),则当x=
(x>0),则当x=![]() =2时,y1+y2=x+
=2时,y1+y2=x+![]() 有最小值为2
有最小值为2![]() =4.
=4.
解决问题
(1)已知函数为y1=x+3(x>﹣3)与函数y2=(x+3)2+9(x>﹣3),当x取何值时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租货使用成本最低?最低是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:如果两个正数a,b,即a>0,b>0,有下面的不等式:![]() ,当且仅当a=b时取到等号我们把
,当且仅当a=b时取到等号我们把![]() 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把![]() 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.
初步探究:(1)已知x>0,求函数y=x+![]() 的最小值.
的最小值.
问题迁移:(2)学校准备以围墙一面为斜边,用栅栏围成一个面积为100m2的直角三角形,作为英语角,直角三角形的两直角边各为多少时,所用栅栏最短?
创新应用:(3)如图,在直角坐标系中,直线AB经点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,求△AOB的内切圆的半径.
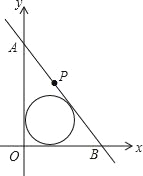
查看答案和解析>>
科目: 来源: 题型:
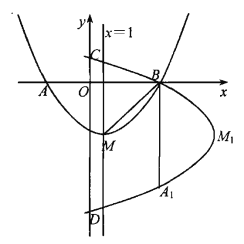
【题目】如图,抛物线y=![]() x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=
x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=![]() x2+bx+c绕点B逆时针方向旋转90°,点M1,A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
x2+bx+c绕点B逆时针方向旋转90°,点M1,A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
(1)写出点B的坐标及求原抛物线的解析式:
(2)求证A,M,A1三点在同一直线上:
(3)设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大.如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(2013年广东梅州11分)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
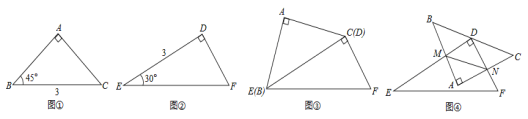
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com