
科目: 来源: 题型:
【题目】在平面直角坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ……按这样的规律进行下去,第1个正方形的面积为_____;第4个正方形的面积为____.
……按这样的规律进行下去,第1个正方形的面积为_____;第4个正方形的面积为____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 在第一象限内的图象相交于点
在第一象限内的图象相交于点![]() .
.

(1)求反比例函数的解析式;
(2)将直线![]() 向上平移后与反比例函数图象在第一象限内交于点
向上平移后与反比例函数图象在第一象限内交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:
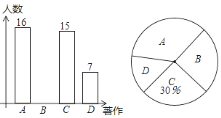
(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】问题探究:
(1)已知:如图①,△ABC中请你用尺规在BC边上找一点D,使得点A到点BC的距离最短.
(2)托勒密(Ptolemy)定理指出,圆的内接四边形两对对边乘积的和等于两条对角线的乘积.如图②,P是正△ABC外接圆的劣弧BC上任一点(不与B、C重合),请你根据托勒密(Ptolemy)定理证明:PA=PB+PC
问题解决:
(3)如图③,某学校有一块两直角边长分别为30m、60m的直角三角形的草坪,现准备在草坪内放置一对石凳及垃圾箱在点P处,使P到A、B、C三点的距离之和最小,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离(结果保留根号);若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线经过![]() ,
,![]() 两点.将
两点.将![]() 绕点
绕点![]() 逆时针旋转90°得到
逆时针旋转90°得到![]() ,点
,点![]() 在抛物线上.
在抛物线上.

(1)求该抛物线的表达式;
(2)已知点![]() 在
在![]() 轴上(点
轴上(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() ,若
,若![]() 与
与![]() 相似,试求点
相似,试求点![]() 的坐标。
的坐标。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,![]() ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.
(1)判断直线ED与⊙O的位置关系,并说明理由;
(2)若CE=1,AC=4,求阴影部分的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙3人聚会,每人带了一件礼物,3件礼物从外盒包装看完全相同,里面的东西只有颜色不同,将3件礼物放在一起.
(1)甲从中随机抽取一件,求甲抽到不是自己带来的礼物的概率;
(2)每人从中随机抽取一件,求甲、乙、丙3人抽到的都不是自己带来的礼物的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20![]() 时,按2元/
时,按2元/![]() 计费;月用水量超过20
计费;月用水量超过20![]() 时,其中的20
时,其中的20![]() 仍按2元/
仍按2元/![]() 收费,超过部分按
收费,超过部分按![]() 元/
元/![]() 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为![]() 时,应交水费
时,应交水费![]() 元.
元.
(1)分别求出![]() 和
和![]() 时
时![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份 | 四月份 | 五月份 | 六月份 |
交费金额 | 30元 | 34元 | 42.6元 |
小明家这个季度共用水多少立方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com