
科目: 来源: 题型:
【题目】在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且
,且![]() .
.
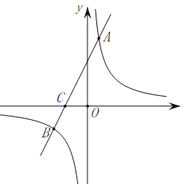
(1)求该反比例函数和一次函数的解析式;
(2)求点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 有最大值,如果存在,请求出点
有最大值,如果存在,请求出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】历下区历史文化悠久,历下一名,取意于大舜帝耕作于历山之下。这位远古圣人为济南留下了影响深远的大舜文化,至今已绵延两千年.某校就同学们对“舜文化”的了解程度进行随机抽样调查,将调查结果绘制成如下两幅统计图:
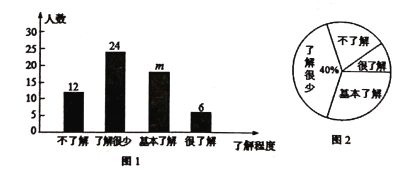
根据统计图的信息,解答下列问题:
(1)本次共调查 名学生,条形统计图中![]() ;
;
(2)若该校共有学生1200名,请估算该校约有多少名学生不了解“舜文化”;
(3)谓查结果中,该校九年级(2)班有四名同学相当优秀,了解程度为“很了解”,他们是三名男生、—名女生,现准备从这四名同学中随机抽取两人去市里参加“舜文化”知识竞赛,用树状或列表法,求恰好抽中一男生一女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形![]() 中,点
中,点![]() 分别在线段
分别在线段![]() 上运动,且满足
上运动,且满足![]() ,
,![]() 分别与
分别与![]() 相交于点
相交于点![]() ,下列说法中:①
,下列说法中:①![]() ;②点
;②点![]() 到线段
到线段![]() 的距离一定等于正方形的边长;③若
的距离一定等于正方形的边长;③若![]() ,则
,则![]() ;④若
;④若![]() ,
,![]() ,则
,则![]() .其中结论正确的是___________;(将正确的序号填写在横线上)
.其中结论正确的是___________;(将正确的序号填写在横线上)
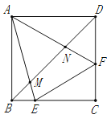
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC 是等边三角形,点 P 在△ABC 内,PA=2,将△PAB 绕点 A 逆时针旋转得到△P1AC,则 P1P 的长等于( )

A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(0<2a≤b)与x轴最多有一个交点.以下四个结论:
①abc>0;
②该抛物线的对称轴在x=﹣1的右侧;
③关于x的方程ax2+bx+c+1=0无实数根;
④![]() ≥2.
≥2.
其中,正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】一张正方形纸的内部被针扎了2010个孔,这些孔和正方形的顶点之中的任何3点都不共线.作若干条互不相交的线段,它们的端点都是这些孔或正方形的顶点,这些线段将正方形分割成一些三角形,并且在这些三角形的内部和边上都不再有小孔.请问一共作了多少条线段?共得到了多少个三角形?
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接北京2022年冬奥会,某工艺厂准备生产奥运会标志与奥运会吉祥物,该厂主要用甲、乙两种原料.已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完.
(1)求该厂能生产奥运会标志和奥运会吉祥物各多少套?
(2)如果奥运会标志的成本为16元,奥运会吉祥物的成本为15元,若东营客商购进奥运会标志和奥运会吉祥物共250件进行试销,其中奥运会标志的件数不大于奥运会吉祥物的件数,且不小于80件,已知奥运会标志的售价为24元/件,奥运会吉祥物的售价为22元/件,且全部售出,设购进奥运会标志m件,求该客商销售这批商品的利润y与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,东营客商决定在试销活动中毎售出一件奥运会标志,就从一件奥运会标志的利润中捐献慈善资金a元,求该客商售完所有商品并捐献资金后获得的最大收益.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形ABCD,F是对角线AC上的一点,过点D作DE∥AC,且DE=CF,连接AE、DE、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BAF+∠AED=180°,求证:四边形ABFE为菱形.
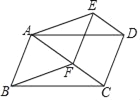
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com