
科目: 来源: 题型:
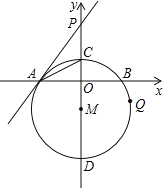
【题目】如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若点C的坐标为(0,2),点A的坐标为(-4,0),
(1)求证:∠PAC=∠CAO;
(2)求直线PA的解析式;
(3)若点Q为⊙M上任意一点,连接OQ、PQ,问![]() 的比值是否发生变化?若不变求出此值;若变化,说明变化规律.
的比值是否发生变化?若不变求出此值;若变化,说明变化规律.
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果店经销一种高档水果,售价为每千克50元
(1)连续两次降价后售价为每千克32元,若每次下降的百分率相同.求平均下降的百分率;
(2)已知这种水果的进价为每千克40元,每天可售出500千克,经市场调查发现,若每千克涨价1元,日销售量将减少20千克,每千克应涨价多少元才能使每天获得的利润最大?
查看答案和解析>>
科目: 来源: 题型:
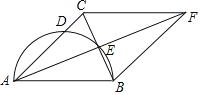
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
查看答案和解析>>
科目: 来源: 题型:
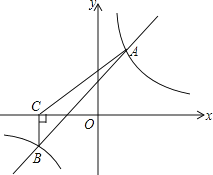
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A(2,3),B(-3,m)两点.
(m≠0)的图象相交于A(2,3),B(-3,m)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为点C,求S△ABC.
查看答案和解析>>
科目: 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)从袋中一次摸出两个球,请用画树状图或列表格的方法列出所有等可能的结果,并求出摸到两个不同颜色球的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如下(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中D小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?

查看答案和解析>>
科目: 来源: 题型:
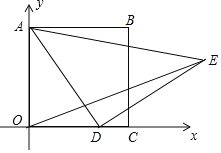
【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
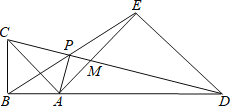
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目: 来源: 题型:
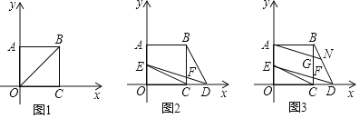
【题目】如图,矩形ABCO在平面直角坐标系中,AO,CO分别在y轴,x轴正半轴上,若S矩形AOCB=![]() BO2,矩形AOCB的周长为16.
BO2,矩形AOCB的周长为16.
(1)求B点坐标;
(2)点D在OC延长线上,设D点横坐标为d,连BD,将直线DB绕D点逆时针方向旋转45°交AO于E,交BC于F,连EC,设△CDE面积=S,求出S与d的函数关系式并注明自变量d的取值范围;
(3)在(2)条件下,当点E在AO上时,过A作ED的平行线交CB于G,交BD于N,若BG=2CF,求S的值.
查看答案和解析>>
科目: 来源: 题型:
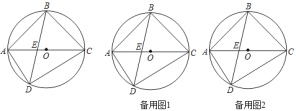
【题目】如图,四边形ABCD内接于⊙O.AC为直径,AC、BD交于E,![]() =
=![]() .
.
(1)求证:AD+CD=![]() BD;
BD;
(2)过B作AD的平行线,交AC于F,求证:EA2+CF2=EF2;
(3)在(2)条件下过E,F分别作AB、BC的垂线垂足分别为G、H,连GH、BO交于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com