
科目: 来源: 题型:
【题目】受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动.为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它”四种类型的设备对学生做了一次抽样调查.调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)若该校共有1500名学生,估计全校用手机上网课的学生共有___________名;
(3)在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.

查看答案和解析>>
科目: 来源: 题型:
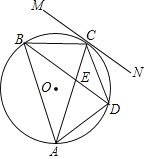
【题目】如图,⊙O为△ABC的外接圆,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.
(1)求证:∠CAB=∠CBD;
(2)若BC=5,BD =8,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
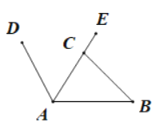
【题目】为倡导“绿色出行,低碳生活”的号召,今年春天,安庆市的街头出现了一道道绿色的风景线--“共享单车”. 图(1)所示的是一辆共享单车的实物图. 图(2)是这辆共享单车的部分几何示意图,其中车架档AC长为40cm,座杆CE的长为18cm. 点A、C、E在同一条直线上,且∠CAB=60°,∠ACB=75°
(1)求车座点E到车架档AB的距离;
(2)求车架档AB的长.

查看答案和解析>>
科目: 来源: 题型:
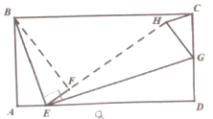
【题目】如图,矩形ABCD中,AB=4,AD=8,点E为AD上一点,将△ABE沿BE折叠得到△FBE,点G为CD上一点,将△DEG沿EG折叠得到△HEG,且E、F、H三点共线,当△CGH为直角三角形时,AE的长为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为![]() 的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
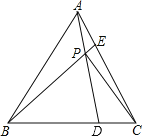
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙M(半径为r),给出如下定义:若点P关于点M的对称点为Q,且r≤PQ≤3r,则称点P为⊙M的称心点.

(1)当⊙O的半径为2时,
①如图1,在点A(0,1),B(2,0),C(3,4)中,⊙O的称心点是 ;
②如图2,点D在直线y![]() x上,若点D是⊙O的称心点,求点D的横坐标m的取值范围;
x上,若点D是⊙O的称心点,求点D的横坐标m的取值范围;
(2)⊙T的圆心为T(0,t),半径为2,直线y![]() x+1与x轴,y轴分别交于点E,F.若线段EF上的所有点都是⊙T的称心点,直接写出t的取值范围.
x+1与x轴,y轴分别交于点E,F.若线段EF上的所有点都是⊙T的称心点,直接写出t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=-2x+mx+n经过点A(0,2),B(3,-4).

(1)求该抛物线的函数表达式及对称轴;
(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A,B两点),如果直线CD与图象G有两个公共点,结合函数的图象,求点D纵坐标t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α(0°<α≤90°),点F,G,P分别是DE,BC,CD的中点,连接PF,PG.
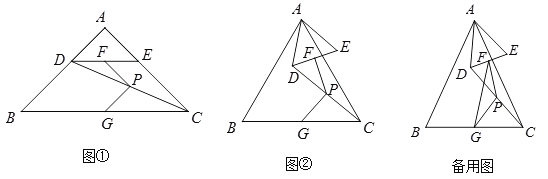
(1)如图①,α=90°,点D在AB上,则∠FPG= °;
(2)如图②,α=60°,点D不在AB上,判断∠FPG的度数,并证明你的结论;
(3)连接FG,若AB=5,AD=2,固定△ABC,将△ADE绕点A旋转,当PF的长最大时,FG的长为 (用含α的式子表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】为了推动全社会自觉尊法学法守法用法,促进全面依法治国,某区每年都举办普法知识竞赛,该区某单位甲、乙两个部门各有员工200人,要在这两个部门中挑选一个部门代表单位参加今年的竞赛,为了解这两个部门员工对法律知识的掌握情况,进行了抽样调查,从甲、乙两个部门各随机抽取20名员工,进行了法律知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息.
a.甲部门成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)
b.乙部门成绩如下:
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
平均数 | 方差 | 中位数 | |
甲 | 79.6 | 36.84 | 78.5 |
乙 | 77 | 147.2 | m |
d.近五年该单位参赛员工进入复赛的出线成绩如下:
2014年 | 2015年 | 2016年 | 2017年 | 2018年 | |
出线成绩(百分制) | 79 | 81 | 80 | 81 | 82 |
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)可以推断出选择 部门参赛更好,理由为 ;
(3)预估(2)中部门今年参赛进入复赛的人数为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com