
科目: 来源: 题型:
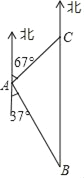
【题目】如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分,根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:

(1)①中的描述应为“6分![]() ”,其中
”,其中![]() 的值为 ;扇形①的圆心角的大小是 ;
的值为 ;扇形①的圆心角的大小是 ;
(2)求这40个样本数据的平均数、众数、中位数;
(3)若该校九年级共有360名学生,估计该校理化实验操作得满分的学生有多少人.
查看答案和解析>>
科目: 来源: 题型:
【题目】解不等式组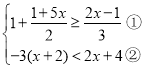
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式维的解集为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+(2﹣a)x﹣2(a>0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.给出下列结论:
①在a>0的条件下,无论a取何值,点A是一个定点;
②在a>0的条件下,无论a取何值,抛物线的对称轴一定位于y轴的左侧;
③y的最小值不大于﹣2;
④若AB=AC,则a=![]() .
.
其中正确的结论有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点p为边AB上的一点,![]() CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
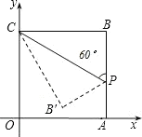
A.(2, 2![]() )B.(
)B.(![]() , 2-2
, 2-2![]() )C.(2, 4-2
)C.(2, 4-2![]() )D.(
)D.(![]() , 4-2
, 4-2![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,△ABC是等腰直角三角形,在两腰AB、AC外侧作两个等边三角形ABD和ACE,AM和AN分别是等边三角形ABD和ACE的角平分线,连接CM、BN,CM与AB交于点P.

(1)求证:CM=BN;
(2)如图②,点F为角平分线AN上一点,且∠CPF=30°,求证:△APF∽△AMC;
(3)在(2)的条件下,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与
,且与![]() 轴交于点C
轴交于点C![]() ,与
,与![]() 轴交于A、B两点(点A在点B的右侧).
轴交于A、B两点(点A在点B的右侧).

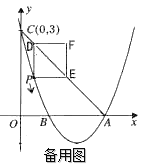
(1)求该抛物线的函数关系式;
(2)点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥![]() 轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
(3)在问题(2)的条件下,P点满足∠DAP=90°,且点E在![]() 轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分9分)如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
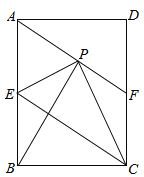
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,正比例函数y=ax的图像与反比例函数![]() 的图像交于点A(3,2).
的图像交于点A(3,2).
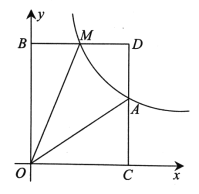
(1)求正比例函数与反比例函数的表达式;
(2)根据图像直接写出在第一象限内,![]() 的x的取值范围;
的x的取值范围;
(3)M(m,n)是反比例函数图像上的一个动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,证:BM=DM.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com