
科目: 来源: 题型:
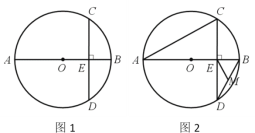
【题目】已知AB是⊙O的直径,C是⊙O上的一点(不与点A,B重合),过点C作AB的垂线交⊙O于点D,垂足为E点.
(1)如图1,当AE=4,BE=2时,求CD的长度;
(2)如图2,连接AC,BD,点M为BD的中点.求证:ME⊥AC.
查看答案和解析>>
科目: 来源: 题型:
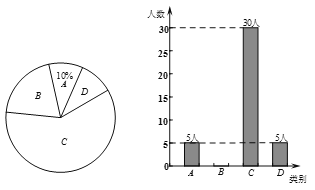
【题目】为了解阳光社区年龄20~60岁居民对垃圾分类的认识,学校课外实践小组随机抽取了该社区、该年龄段的部分居民进行了问卷调查,并将调查数据整理后绘成如下两幅不完整的统计图.图中A表示“全部能分类”,B表示“基本能分类”,C表示“略知一二”,D表示“完全不会”.请根据图中信息解答下列问题:
(1)补全条形统计图并填空:被调查的总人数是 人,扇形图中D部分所对应的圆心角的度数为 ;
(2)若该社区中年龄20~60岁的居民约3000人,请根据上述调查结果,估计该社区中C类有多少人?
(3)根据统计数据,结合生活实际,请你对社区垃圾分类工作提一条合理的建议.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,漏壶是一种古代计时器.在它内部盛一定量的水,水从壶下的小孔漏出.壶内壁有刻度,人们根据壶中水面的位置计算时间.用x(小时)表示漏水时间,y(厘米)表示壶底到水面的高度,某次计时过程中,记录到部分数据如下表:
漏水时间x(小时) | … | 3 | 4 | 5 | 6 | … |
壶底到水面高度y(厘米) | … | 9 | 7 | 5 | 3 | … |
(1)问y与x的函数关系属于一次函数、二次函数和反比例函数中的哪一种?求出该函数解析式及自变量x的取值范围;
(2)求刚开始计时时壶底到水面的高度.
查看答案和解析>>
科目: 来源: 题型:
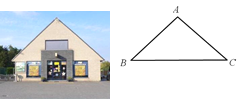
【题目】等腰三角形的屋顶,是建筑中经常采用的结构形式.在如图所示的等腰三角形屋顶ABC中,AB=AC,测得BC=20米,∠C=41°,求顶点A到BC边的距离是多少米?(结果精确到0.1米.参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869.)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,BC=6,DE是△ABC的中位线,点D在AB上,把点B绕点D按顺时针方向旋转α(0°<α<180°)角得到点F,连接AF,BF.下列结论:①△ABF是直角三角形;②若△ABF和△ABC全等,则α=2∠BAC或2∠ABC;③若α=90°,连接EF,则S△DEF=4.5;其中正确的结论是( )
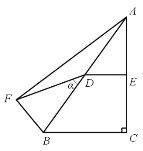
A.①②B.①③C.①②③D.②③
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x kg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元, y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
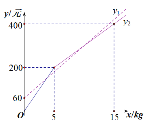
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5 kg后,超过的部分价格优惠是打五折
D.若顾客采摘12 kg草莓,那么到甲园或乙园的总费用相同
查看答案和解析>>
科目: 来源: 题型:
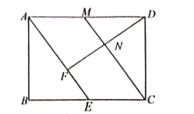
【题目】如图,在矩形![]() 中,点E为
中,点E为![]() 的中点,连接
的中点,连接![]() ,过点D作
,过点D作![]() 于点F,过点C作
于点F,过点C作![]() 于点N,延长
于点N,延长![]() 交
交![]() 于点M.
于点M.
(1)求证:![]()
(2)连接CF,并延长CF交AB于G
①若![]() ,求
,求![]() 的长度;
的长度;
②探究当![]() 为何值时,点G恰好为AB的中点.
为何值时,点G恰好为AB的中点.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种杂交柑橘新品种,皮薄汁多,口感细嫩,风味极佳,深受怎么喜爱,某果农种植销售过程中发现,这种柑橘的种植成本为6元/千克,日销量![]() 与销售单价
与销售单价![]() (元)之间存在一次函数关系,如图所示
(元)之间存在一次函数关系,如图所示
(1)求![]() 与
与![]() 之间的函数关系式
之间的函数关系式
(2)该果农每天销售这种柑橘不低于60千克且不超过150千克,试求其销售单价定为多少时,除去种植成本后,每天销售利润最大?最大利润是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】九年级某班联欢会上,节目组设计了一个即兴表演节目游戏,在一个不透明的盒子里,放有五个完全相同的乒乓球,乒乓球上分别标有数字1,2,3,4,5,游戏规则是:参加联欢会的50名同学,每人同时从盒子里一次摸出两个乒乓球,若两球上数字之和是偶数就给大家即兴表演一个节目;否则,下一个同学依次进行,直至50名同学都模完,
(1)若小朱是该班同学,用列表法或画树状图法求小朱同学表演节目的概率
(2)若参加联欢会的同学每人都有一次摸球的机会,请估计本次联欢会上有多少个同学表演节目?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com