
科目: 来源: 题型:
【题目】如图,重庆欢乐谷的摩天轮是西南地区最高的摩天轮,号称“重庆之限”.摩天轮是一个圆形,直径AB垂直水平地面于点C,最低点B离地面的距离BC为1.6米.某天,妈妈带着洋洋来坐摩天轮,当她站在点D仰着头看见摩天轮的圆心时,仰角为37,为了选择更佳角度为洋洋拍照,妈妈后退了49米到达点D’,当洋洋坐的桥厢F与圆心O在同一水平线时,他俯头看见妈妈的眼睛,此时俯角为42,已知妈妈的眼睛到地面的距离为1.6米,妈妈两次所处的位置与摩天轮在同一平面上,则该摩天轮最高点A离地面的距离AC约是( )
(参考数据:sin37≈0.60,tan37≈0.75,sin42≈0.67,tan42≈0.90)
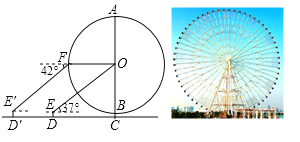
A.118.8米B.127.6米C.134.4米D.140.2米
查看答案和解析>>
科目: 来源: 题型:
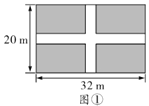
【题目】为了美化校园,某校要在如图①所示的长![]() ,宽
,宽![]() 的矩形地面上修等宽的人行道,余下的部分进行绿化.
的矩形地面上修等宽的人行道,余下的部分进行绿化.
(1)设人行道宽为![]() ,用含
,用含![]() 的式子表示绿化面积;
的式子表示绿化面积;
(2)如果要使绿化面积为![]() ,求出此时人行道的宽;
,求出此时人行道的宽;
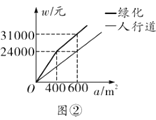
(3)已知某园林公司修筑人行道、绿化的造价![]() (元)、
(元)、![]() (元)与修建面积
(元)与修建面积![]() 之间的函数关系如图②所示,如果该校决定由该公司承建此项目,并要求修建的人行道的宽度不少于
之间的函数关系如图②所示,如果该校决定由该公司承建此项目,并要求修建的人行道的宽度不少于![]() 且不超过
且不超过![]() ,那么人行道宽为多少时,修建的人行道和绿化的总造价最低,最低总造价为多少元?
,那么人行道宽为多少时,修建的人行道和绿化的总造价最低,最低总造价为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,一条直线
,一条直线![]() 与边
与边![]() 相交于点
相交于点![]() ,与边
,与边![]() 相交于点
相交于点![]() .
.
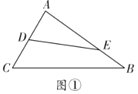
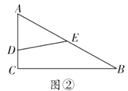
(1)如图①,若![]() 将
将![]() 分成周长相等的两部分,求
分成周长相等的两部分,求![]() 的值;(用
的值;(用![]() 、
、![]() 、
、![]() 表示)
表示)
(2)如图②,若![]() ,
,![]() ,
,![]() ,
,![]() 将
将![]() 分成周长、面积相等的两部分,求
分成周长、面积相等的两部分,求![]() 的值;
的值;
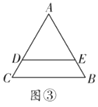
(3)如图③,若![]() 将
将![]() 分成周长、面积相等的两部分,且
分成周长、面积相等的两部分,且![]() ,则
,则![]() 、
、![]() 、
、![]() 满足什么关系?
满足什么关系?
查看答案和解析>>
科目: 来源: 题型:
【题目】小亮看到路边上有人设摊玩“有奖掷币”游戏,规则是交2元钱可以玩一次掷硬币游戏,每次同时掷两枚硬币,如果出现两枚硬币都正面朝上,奖金5元;如果是其他情况,则没有奖金(每枚硬币落地只有正面朝上和反面朝上两种情况).
(1)小亮应不应该玩?
(2)如果有100人,每人玩一次这种游戏,设摊者约获利多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 、
、![]() 是紧靠某湖泊的两条相互垂直的公路,曲线段
是紧靠某湖泊的两条相互垂直的公路,曲线段![]() 是该湖泊环湖观光大道的一部分.现准备修建一条直线型公路
是该湖泊环湖观光大道的一部分.现准备修建一条直线型公路![]() ,用以连接两条公路和环湖观光大道,且直线
,用以连接两条公路和环湖观光大道,且直线![]() 与曲线段
与曲线段![]() 有且仅有一个公共点
有且仅有一个公共点![]() .已知点
.已知点![]() 到
到![]() 、
、![]() 的距离分别为
的距离分别为![]() 和
和![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() .若分别以
.若分别以![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,则曲线段
,则曲线段![]() 对应的函数解析式为
对应的函数解析式为![]() .
.
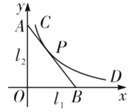
(1)求![]() 的值,并指出函数
的值,并指出函数![]() 的自变量的取值范围;
的自变量的取值范围;
(2)求直线![]() 的解析式,并求出公路
的解析式,并求出公路![]() 的长度(结果保留根号).
的长度(结果保留根号).
查看答案和解析>>
科目: 来源: 题型:
【题目】位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1:![]() ,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:
,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .给出以下四个结论:
.给出以下四个结论:
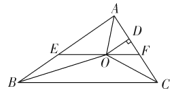
①若![]() ,
,![]() ;
;
②![]() ;
;
③![]() 平分
平分![]() ;
;
④若![]() ,
,![]() ,则
,则![]() .
.
其中正确的有________.(把所有正确结论的序号都选上)
查看答案和解析>>
科目: 来源: 题型:
【题目】两个全等的等腰直角三角形,斜边长为2,按如图放置,其中一个三角形45°角的项点与另一个三角形的直角顶点A重合,若三角形ABC固定,当另一个三角形绕点A旋转时,它的角边和斜边所在的直线分别与边BC交于点E、F,设BF=![]() CE=
CE=![]() 则
则![]() 关于
关于![]() 的函数图象大致是( )
的函数图象大致是( )
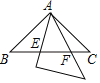
A.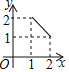 B.
B.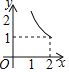 C.
C.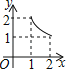 D.
D.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题探究
(1)如图1.在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() .则
.则![]() 面积的最大值是_______.
面积的最大值是_______.
(2)如图2,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的高,
边上的高,![]() 为
为![]() 的外接圆,若
的外接圆,若![]() ,试判断
,试判断![]() 是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.
是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.
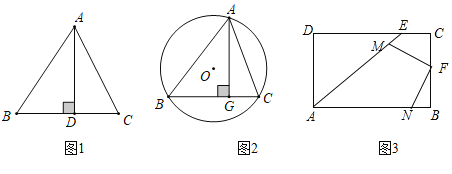
问题解决:
如图3,王老先生有一块矩形地![]() ,
,![]() ,
,![]() ,现在他想利用这块地建一个四边形鱼塘
,现在他想利用这块地建一个四边形鱼塘![]() ,且满足点
,且满足点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,这个四边形
,这个四边形![]() 的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com