
科目: 来源: 题型:
【题目】如图,D是△ABC内一点,BD⊥CD,E、F、G、H分别是边AB、BD、CD、AC的中点.若AD=10,BD=8,CD=6,则四边形EFGH的周长是( )
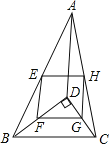
A.24B.20C.12D.10
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,记函数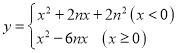 的图象为
的图象为![]() ,正方形
,正方形![]() 的对称中心与原点重合,顶点
的对称中心与原点重合,顶点![]() 的坐标为(2,2),点
的坐标为(2,2),点![]() 在第四象限.
在第四象限.
(1)当![]() =1时.
=1时.
①求![]() 的最低点的纵坐标;
的最低点的纵坐标;
②求图象![]() 上所有到
上所有到![]() 轴的距离为2的横坐标之和.
轴的距离为2的横坐标之和.
③若当![]() ≤
≤![]() ≤
≤![]() 时,-9≤
时,-9≤![]() ≤2,则
≤2,则![]() 、
、![]() 的对应值为 .
的对应值为 .
(2)当图象![]() 与正方形
与正方形![]() 的边恰好有两个公共点时,直接写出
的边恰好有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△![]() 中,高
中,高![]() =3,∠
=3,∠![]() =45°,
=45°,![]() =
=![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位长度的速速向终点
方向以每秒1个单位长度的速速向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 、
、![]() 的平行线,与
的平行线,与![]() 分别交于点
分别交于点![]() 、
、![]() ,将△
,将△![]() 绕
绕![]() 的中点旋转180°得△
的中点旋转180°得△![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,△
秒,△![]() 与△
与△![]() 重叠部分面积为
重叠部分面积为![]() .
.
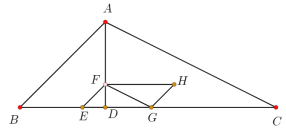
(1)当![]() = 秒时,点
= 秒时,点![]() 落在
落在![]() 边上.
边上.
(2)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当直线![]() 将△
将△![]() 分为面积比为1:3的两部分时,直接写出
分为面积比为1:3的两部分时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践:折纸中的数学
问题情境:
在矩形![]() 中,
中,![]() =12,点
=12,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() =
=![]() ,将△
,将△![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点
的对应点为点![]() ,将△
,将△![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点Q,且点
的对应点为点Q,且点![]() 、
、![]() 均落在矩形
均落在矩形![]() 的内部(如图①).
的内部(如图①).
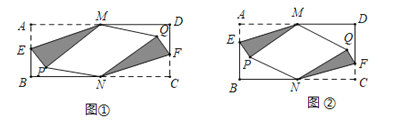
数学思考:
(1)判断![]() 与
与![]() 是否平行,并说明理由;
是否平行,并说明理由;
(2)当![]() 长度是多少时,存在点
长度是多少时,存在点![]() ,使四边形
,使四边形![]() 是有一个内角为60°的菱形(如图②)?直接写出
是有一个内角为60°的菱形(如图②)?直接写出![]() 的长度及菱形
的长度及菱形![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个高都是10cm的圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6![]() ,管子的体积忽略不计),、现在三个容器中,只有甲中有水,水位高2
,管子的体积忽略不计),、现在三个容器中,只有甲中有水,水位高2![]() ,如图①所示,若每分钟同时向乙、丙中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位
,如图①所示,若每分钟同时向乙、丙中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位![]() (
(![]() )与注水时间
)与注水时间![]() (
(![]() )的图象如图②所示.
)的图象如图②所示.
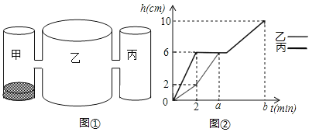
(1)乙、丙两个容器的底面积之比为 .
(2)图②中![]() 的值为 ,
的值为 ,![]() 的值为 .
的值为 .
(3)注水多少分钟后,乙与甲的水位相差2![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
【题目】工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,请将下列过程补充完整:
收集数据:
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:

整理、描述数据:
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70—79分为生产技能良好,60—69分为生产技能合格,60分以下为生产技能不合格)
分析数据:
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | |
乙 | 78 | 81 |
得出结论:
![]() .估计乙部门生产技能优秀的员工人数约为 .
.估计乙部门生产技能优秀的员工人数约为 .
![]() .可以推断出 部门员工的生产技能水平高.理由为 .
.可以推断出 部门员工的生产技能水平高.理由为 .
(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目: 来源: 题型:
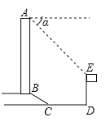
【题目】如图,某办公大楼正前方有一根高度是15米的旗杆![]() ,从办公大楼顶端
,从办公大楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是45°,旗杆底端
是45°,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是10米,梯坎坡长
是10米,梯坎坡长![]() 是10米,梯坎坡度
是10米,梯坎坡度![]() =1:
=1:![]() ,则大楼
,则大楼![]() 的高为______米.
的高为______米.
查看答案和解析>>
科目: 来源: 题型:
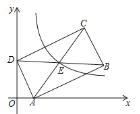
【题目】在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() (1,0),
(1,0),![]() (0,2),点
(0,2),点![]() 在第一象限,
在第一象限,![]() ∥
∥![]() 轴,若函数
轴,若函数![]() =
=![]() 的图象经过矩形
的图象经过矩形![]() 的对角线的交点,则
的对角线的交点,则![]() 的值为( )
的值为( )
A.4B.5C.8D.10
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数![]() 的顶点
的顶点![]() 是直线
是直线![]() 和直线
和直线![]() 的交点.
的交点.
(1)用含![]() 的代数式表示顶点
的代数式表示顶点![]() 的坐标.
的坐标.
(2)①当![]() 时,
时,![]() 的值均随
的值均随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
②若![]() ,且
,且![]() 满足
满足![]() 时,二次函数的最小值为
时,二次函数的最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)试证明:无论![]() 取任何值,二次函数
取任何值,二次函数![]() 的图象与直线
的图象与直线![]() 总有两个不同的交点.
总有两个不同的交点.
查看答案和解析>>
科目: 来源: 题型:
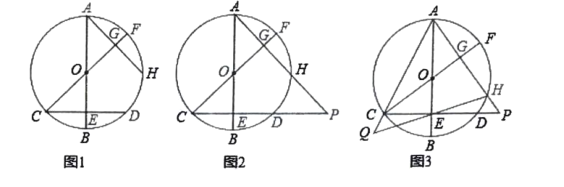
【题目】已知:![]() 都是
都是![]() 的直径,
的直径,![]() 都是
都是![]() 的弦,
的弦,![]() 于点
于点![]() ,
,![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,延长![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,延长![]() ,
,![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com