
科目: 来源: 题型:
【题目】2020年新冠肺炎疫情发生以来,我市广大在职党员积极参与社区防疫工作,助力社区坚决打赢疫情防控阻击战.其中,![]() 社区有500名在职党员,为了解本社区2月-3月期间在职党员参加应急执勤的情况,
社区有500名在职党员,为了解本社区2月-3月期间在职党员参加应急执勤的情况,![]() 社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.
社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.

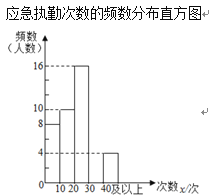
其中,应急执勤次数在![]() 这一组的数据是:
这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)![]() ______,
______,![]() ______;
______;
(2)请补全频数分布直方图;
(3)随机抽取的50名在职党员参加应急执勤次数的中位数是______;
(4)请估计2月-3月期间![]() 社区在职党员参加应急执勤的次数不低于30次的约有______人.
社区在职党员参加应急执勤的次数不低于30次的约有______人.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
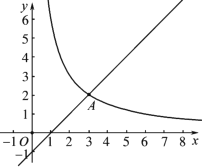
(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是
是![]() 轴上的一点,过点
轴上的一点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() .横、纵坐标都是整数的点叫做整点.记
.横、纵坐标都是整数的点叫做整点.记![]() 的图象在点
的图象在点![]() ,
,![]() 之间的部分与线段
之间的部分与线段![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点的坐标为______;
内的整点的坐标为______;
②若区域![]() 内恰有6个整点,结合函数图象,求出
内恰有6个整点,结合函数图象,求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小菲设计的“作一个角等于已知角的二倍”的尺规作图过程.
已知:![]() 中,
中,![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如图,
①分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ;
;
②分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ,
,![]() 和
和![]() 交于点
交于点![]() ;
;
③连接![]() 和
和![]() ;
;
④以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() .
.
所以![]() .
.
根据小菲设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);

(2)完成下面的证明.
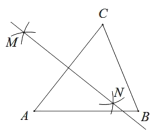
证明:连接![]()
∵![]() 和
和![]() 分别为
分别为![]() 、
、![]() 的垂直平分线,
的垂直平分线,
∴![]() ________.
________.
∴![]() 是
是![]() 的外接圆.
的外接圆.
∵点![]() 是
是![]() 上的一点,
上的一点,
∴![]() .(____________).(填推理的依据)
.(____________).(填推理的依据)
查看答案和解析>>
科目: 来源: 题型:
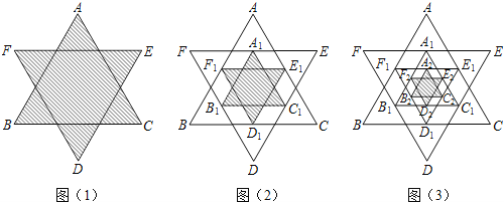
【题目】如图(1) ,将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和1D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E 2F 2,如图(3) 中阴影部分;如此下去…,则正六角星形AnFnBnDnCnE nF n的面积为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】为提升英语听力及口语技能,小明打算在手机上安装一款英语口语APP辅助练习.他分别从甲、乙、丙三款口语APP中随机选取了1000条网络评价进行对比,统计如下:
等级 评价数量 APP | 五星 | 四星 | 三星 | 二星 | 一星 | 合计 |
甲 | 562 | 286 | 79 | 48 | 25 | 1000 |
乙 | 517 | 393 | 52 | 21 | 17 | 1000 |
丙 | 504 | 210 | 136 | 116 | 34 | 1000 |
(说明:网上对于口语APP的综合评价从高到低依次为五星、四星、三星、二星和一星).
小明选择________(填“甲”、“乙”或“丙”)款英语口语APP,能获得良好口语辅助练习(即评价不低于四星)的可能性最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为![]() ,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:
,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】对于平面直角坐标系xOy中的任意点![]() ,如果满足
,如果满足![]() (x≥0,a为常数),那么我们称这样的点叫做“特征点”.
(x≥0,a为常数),那么我们称这样的点叫做“特征点”.
(1)当2≤a≤3时,
①在点![]() 中,满足此条件的特征点为__________________;
中,满足此条件的特征点为__________________;
②⊙W的圆心为![]() ,半径为1,如果⊙W上始终存在满足条件的特征点,请画出示意图,并直接写出m的取值范围;
,半径为1,如果⊙W上始终存在满足条件的特征点,请画出示意图,并直接写出m的取值范围;
(2)已知函数![]() ,请利用特征点求出该函数的最小值.
,请利用特征点求出该函数的最小值.
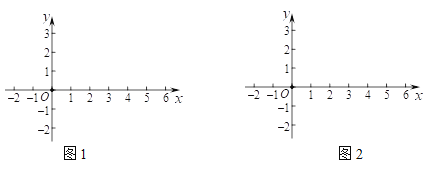
查看答案和解析>>
科目: 来源: 题型:
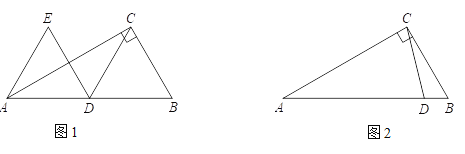
【题目】在△ABC中,∠ACB=90°,∠CAB=30°,点D在AB上,连接CD,并将CD绕点D逆时针旋转60°得到DE,连接AE.
(1)如图1,当点D为AB中点时,直接写出DE与AE长度之间的数量关系;
(2)如图2,当点D在线段AB上时,
① 根据题意补全图2;
② 猜想DE与AE长度之间的数量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数![]() 的图象与y轴交于点A,与抛物线
的图象与y轴交于点A,与抛物线![]() 的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
(1)求出抛物线的对称轴和点C坐标;
(2)①当![]() 时,直接写出抛物线
时,直接写出抛物线![]() 与图形G的公共点个数.
与图形G的公共点个数.
②如果抛物线![]() 与图形G有且只有一个公共点,求出a的取值范围.
与图形G有且只有一个公共点,求出a的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com