
科目: 来源: 题型:
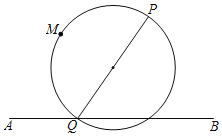
【题目】如图,平面上存在点P、点M与线段AB.若线段AB上存在一点Q,使得点M在以PQ为直径的圆上,则称点M为点P与线段AB的共圆点.
已知点P(0,1),点A(﹣2,﹣1),点B(2,﹣1).
(1)在点O(0,0),C(﹣2,1),D(3,0)中,可以成为点P与线段AB的共圆点的是 ;
(2)点K为x轴上一点,若点K为点P与线段AB的共圆点,请求出点K横坐标xK的取值范围;
(3)已知点M(m,﹣1),若直线y=![]() x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
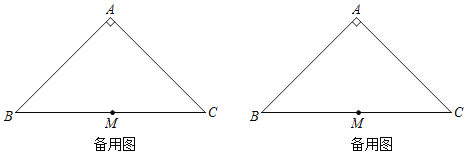
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,点M为BC中点.点P为AB边上一动点,点D为BC边上一动点,连接DP,以点P为旋转中心,将线段PD逆时针旋转90°,得到线段PE,连接EC.
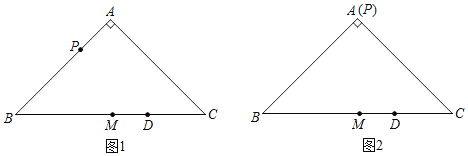
(1)当点P与点A重合时,如图2.
①根据题意在图2中完成作图;
②判断EC与BC的位置关系并证明.
(2)连接EM,写出一个BP的值,使得对于任意的点D总有EM=EC,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=ax2+bx﹣1交y轴于点P.
(1)过点P作与x轴平行的直线,交抛物线于点Q,PQ=4,求![]() 的值;
的值;
(2)横纵坐标都是整数的点叫做整点.在(1)的条件下,记抛物线与x轴所围成的封闭区域(不含边界)为W.若区域W内恰有4个整点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
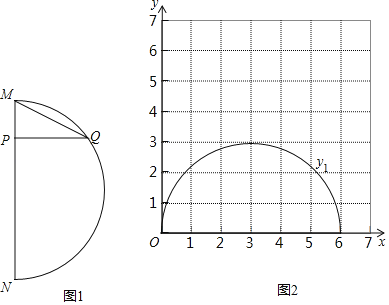
【题目】如图1,在弧MN和弦MN所组成的图形中,P是弦MN上一动点,过点P作弦MN的垂线,交弧MN于点Q,连接MQ.已知MN=6cm,设M、P两点间的距离为xcm,P、Q两点间的距离为y1cm,M、Q两点间的距离为y2cm.小轩根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小轩的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:x/cm.
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.24 | 2.83 | 3.00 | 2.83 | 2.24 | 0 |
y2/cm | 0 | 2.45 | 3.46 | 4.24 | m | 5.48 | 6 |
上表中m的值为 .(保留两位小数)
(2)在同一平面直角坐标系xOy(图2)中,函数y1的图象如图,请你描出补全后的表中y2各组数值所对应的点(x,y2),并画出函数y2的图象;
(3)结合函数图象,解决问题:当△MPQ有一个角是30°时,MP的长度约为 cm.(保留两位小数)
查看答案和解析>>
科目: 来源: 题型:
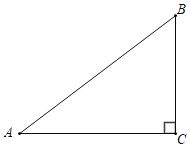
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O交AB于点D,线段BC上有一点P.
(1)当点P在什么位置时,直线DP与⊙O有且只有一个公共点,补全图形并说明理由.
(2)在(1)的条件下,当BP=![]() ,AD=3时,求⊙O半径.
,AD=3时,求⊙O半径.
查看答案和解析>>
科目: 来源: 题型:
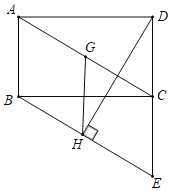
【题目】如图,矩形ABCD,过点B作BE∥AC交DC的延长线于点E.过点D作DH⊥BE于H,G为AC中点,连接GH.
(1)求证:BE=AC.
(2)判断GH与BE的数量关系并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息:

a.截止3月1日20时,全国已有11个省份工业企业复工率在90%以上,主要位于东南沿海地区,位居前三的分别是贵州(100%)、浙江(99.8%)、江苏(99%).
b.各省份复工率数据的频数分布直方图如图1(数据分成6组,分别是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c.如图2,在b的基础上,画出扇形统计图:
d.截止到2020年3月1日各省份的复工率在80<x≤90这一组的数据是:
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e.截止到2020年3月1日各省份的复工率的平均数、中位数、众数如下:
日期 | 平均数 | 中位数 | 众数 |
截止到2020年3月1日 | 80.79 | m | 50,90 |
请解答以下问题:
(1)依据题意,补全频数分布直方图;
(2)扇形统计图中50<x≤60这组的圆心角度数是 度(精确到0.1).
(3)中位数m的值是 .
(4)根据以上统计图表简述国内企业截止3月1日的复工率分布特征.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=2x﹣1的图象交于A、B两点,已知A(m,﹣3).
的图象与一次函数y=2x﹣1的图象交于A、B两点,已知A(m,﹣3).
(1)求k及点B的坐标;
(2)若点C是y轴上一点,且S△ABC=5,直接写出点C的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小方设计的“作一个30°角”的尺规作图过程.
已知:直线AB及直线AB外一点P.
求作:直线AB上一点C,使得∠PCB=30°.
作法:
①在直线AB上取一点M;
②以点P为圆心,PM为半径画弧,与直线AB交于点M、N;
③分别以M、N为圆心,PM为半径画弧,在直线AB下方两弧交于点Q.
④连接PQ,交AB于点O.
⑤以点P为圆心,PQ为半径画弧,交直线AB于点C且点C在点O的左侧.则∠PCB就是所求作的角.
根据小方设计的尺规作图过程,
(1)使用直尺和圆规补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵PM=PN=QM=QN,
∴四边形PMQN是 .
∴PQ⊥MN,PQ=2PO( ).(填写推理依据)
∵在Rt△POC中,sin∠PCB=![]() = (填写数值)
= (填写数值)
∴∠PCB=30°.

查看答案和解析>>
科目: 来源: 题型:
【题目】ABCD中,对角线AC、BD相交于点O,E是边AB上的一个动点(不与A、B重合),连接EO并延长,交CD于点F,连接AF,CE,下列四个结论中:
①对于动点E,四边形AECF始终是平行四边形;
②若∠ABC<90°,则至少存在一个点E,使得四边形AECF是矩形;
③若AB>AD,则至少存在一个点E,使得四边形AECF是菱形;
④若∠BAC=45°,则至少存在一个点E,使得四边形AECF是正方形.
以上所有正确说法的序号是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com