【题目】在抗击新冠肺炎疫情期间，市场上防护口罩出现热销．某药店用元购进甲，乙两种不同型号的口罩共个进行销售，已知购进甲种口罩与乙种口罩的费用相同，购进甲种口罩单价是乙种口罩单价的倍．

求购进的甲，乙两种口罩的单价各是多少？

若甲，乙两种口罩的进价不变，该药店计划用不超过元的资金再次购进甲，乙两种口罩共个，求甲种口罩最多能购进多少个？

【题目】《中学生体质健康标准》规定学生体质健康等级标准： 分及以上为优秀； 分分为良好； 分分为及格；分以下为不及格．某校为了解学生的体质健康情况，从八年级学生中随机抽取了的学生进行了体质测试，并将测试数据制成如下统计图．请根据相关信息解答下面的问题：

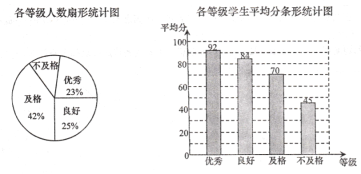
扇形统计图中，“不及格” 等级所在扇形圆心角的度数是多少？

求参加本次测试学生的平均成绩；

若参加本次测试“良好”及“良好”以上等级的学生共有人，请你估计全校八年级“不及格”等级的学生大约有多少人．

【题目】如图，是边长为的等边三角形，将绕边的中点逆时针旋转，点的运动路径为，则图中阴影部分的面积为__________．

【题目】疫情无情人有情，爱心捐款传真情．新冠肺炎疫情发生后，某班学生积极参加献爱心活动，该班名学生的捐款统计情况如下表，关于捐款金额，下列说法错误的是（ ）

A.平均数为元B.众数为元C.中位数为元D.极差为元

【题目】定义：在平面直角坐标系中，某个函数图象上任意两点的坐标分别为（x1，y1），（x2，y2），且x1≤x2，d=|y1-y2|．将这个函数图象在直线y=y1下方部分沿直线y=y1翻折，并将其向上平移d个单位，将这部分图象与原函数图象剩余部分的图象组成的新图象记为G，图象G对应的函数叫做这个函数的伴随函数．例如：点A（1，0）、B（2，1）在一次函数y=x-1的图象上，则它的伴随函数为．

（1）点A、B在直线y=-2x上，点A在第二象限，点B在x轴上．当d=2时，求函数y=-2x的伴随函数所对应的函数表达式．

（2）二次函数y=x2-2x-3的图象交x轴负半轴交于点A，点B在抛物线上，设点B的横坐标为m．

①当d=0时，求该抛物线的伴随函数的图象G与直线y=4在第一象限的交点坐标；

②若直线y=2与该抛物线的伴随函数的图象G有四个交点，直接写出m的取值范围．

（3）抛物线y=x2-2nx+n2-n-1与y轴交于点A，点B在点A的左侧抛物线上，且d=1，当该抛物线的伴随函数的图象G上的点到x轴距离的最小值为1时，直接写出n的值．

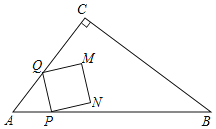
（1）当点Q在边AC上时，用含t的代数式表示PQ的长．

（2）当点M落在边BC上时，求t的值．

（3）当点Q在边AC上时，设正方形PQMN与△ABC重叠部分图形的面积为S，求S与t之间的函数关系式．

（4）当正方形PQMN的边QM被△ABC的边平分时，直接写出t的值．

（探究）当点E落在线段DF上时，CD与BE交于点G．其它条件不变，如图②．

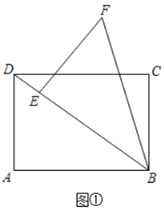
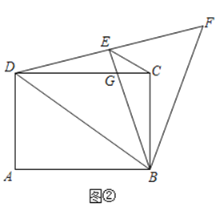
（1）求证：△ADB≌△EDB；

（2）CG的长为______．

（拓展）连结CF，在△BAD的旋转过程中，设△CEF的面积为S，直接写出S的取值范围．

（1）快递车从伊通到长春的速度是______km/h，往返长春和靖宇两地一共用时______h．

（2）当这辆快递车在靖宇到伊通的路段上行驶时，求y与x之间的函数关系式，并写出自变量x的取值范围．

（3）如果这辆快递车两次经过同一个服务区的时间间隔为4h，直接写出这个服务区距离伊通的路程．

【题目】如图，E是的斜边AB上一点，以AE为直径的与边BC相切于点D，交边AC于点F，连结AD．

（1）求证：AD平分．

（2）若，，求的长．