
科目: 来源: 题型:
【题目】已知在平面直角坐标中,点A(m,n)在第一象限内,AB⊥OA且AB=OA,反比例函数y=![]() 的图象经过点A,
的图象经过点A,
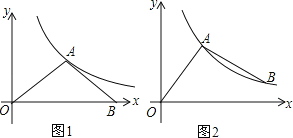
(1)当点B的坐标为(4,0)时(如图1),求这个反比例函数的解析式;
(2)当点B在反比例函数y=![]() 的图象上,且在点A的右侧时(如图2),用含字母m,n的代数式表示点B的坐标;
的图象上,且在点A的右侧时(如图2),用含字母m,n的代数式表示点B的坐标;
(3)在第(2)小题的条件下,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】经中共中央决定设立河北雄安新区,这一重大措施必将带动首都及周边区域向更高水平发展,同时也会带来更多商机.某水果经销商在第一周购进一批水果1160件,预计在第二周进行试销,购进价格为每件10元,若售价为每件12元,则可全部售出;若售价每涨价0.1元,销量就减少2件.
(1)若该经销商在第二周的销量不低于1100件,则售价应不高于多少元?
(2)由于销量较好,第三周水果进价比第一周每件增加了20%,该经销商增加了进货量,并加强了宣传力度,结果第三周的销量比第二周在(1)条件下的最低销量增加了m%,但售价比第二周在(1)条件下的最高售价减少了![]() m%,结果第三周利润达到3388元,求m的值(m>10).
m%,结果第三周利润达到3388元,求m的值(m>10).
查看答案和解析>>
科目: 来源: 题型:
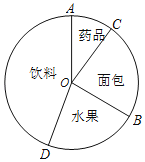
【题目】参加学校运动会,八年级1班第一天购买了水果,面包,饮料,药品等四种食品,四种食品购买金额的统计图表如图所示,若将水果、面包、药品三种食品统称为非饮料食品,并规定t=![]() .
.
(1)①求t的值;![]()
②求扇形统计图中钝角∠AOB的度数.
(2)根据实际需要,该班第二天购买这四种食品时,增加购买饮料金额,同时减少购买面包金额,假设增加购买饮料金额的25%等于减少购买面包的金额,且购买面包的金额不少于100元,求t的取值范围.
金额 食品 | 金额(单位:元) |
水果 | 100 |
面包 | 125 |
饮料 | 225 |
药品 | 50 |
查看答案和解析>>
科目: 来源: 题型:
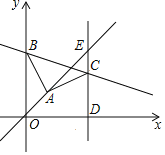
【题目】如图,平面直角坐标系中,A(4,4),B为y轴正半轴上一点,连接AB,在第一象限作AC=AB,∠BAC=90°,过点C作直线CD⊥x轴于D,直线CD与直线y=x交于点E,且ED=5EC,则直线BC解析式为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,折叠矩形![]() 的一边
的一边![]() ,使点
,使点![]() 落在
落在![]() 边的点
边的点![]() 处,折痕为
处,折痕为![]() ,连接
,连接![]() .已知点
.已知点![]() 的坐标为
的坐标为![]() ,二次函数
,二次函数![]() 图象经过
图象经过![]() 、
、![]() 、
、![]() 三点.
三点.
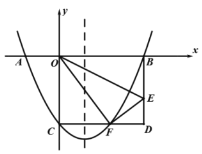
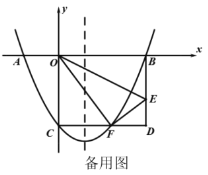
(1)求函数解析式;
(2)在![]() 轴下方抛物线上有一动点
轴下方抛物线上有一动点![]() ,过点
,过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,当
,当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
(3)在抛物线对称轴上是否存在一点![]() ,使
,使![]() 有最大值?若存在,请直接写出
有最大值?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
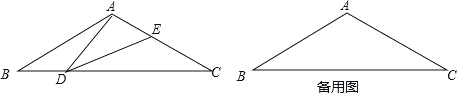
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】德州扒鸡闻名全国,远销海外,被誉为“天下第一鸡”.某种德州扒鸡其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售量可增加20千克,若该专卖店销售这种扒鸡想要平均每天获利2240元,请回答:
(1)每千克这种扒鸡应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,贏得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目: 来源: 题型:
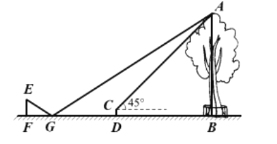
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
查看答案和解析>>
科目: 来源: 题型:
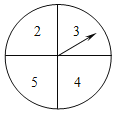
【题目】如图所示,有一个可以自由转动的转盘,其盘面分为4等份,在每一等份分别标有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次,每一次停止后,小明将指针所指数字记录如下:
次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
数字 | 3 | 5 | 2 | 3 | 3 | 4 | 3 | 5 |
(1)求前8次的指针所指数字的平均数.
(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大于3.5”的结果?若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面等分线时为无效转次.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com