
科目: 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) | x60 | x |
售价(元/件) | 200 | 100 |
若用1800元购进甲种商品的件数与用900元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共100件,其中销售甲种商品为a件(a40),设销售完100件甲、乙两种商品的总利润为w元,求w与a之间的函数关系式,并求出w的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年,由于“疫情”的原因,学校未能准时开学,某中学为了了解学生在家“课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 6 |
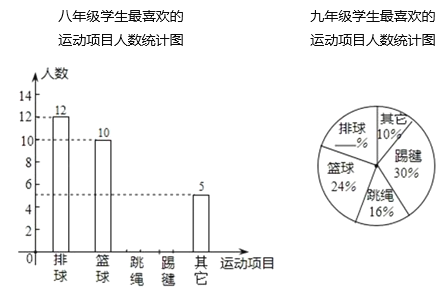
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取的人数为 人;
(2)请直接补全统计表和统计图;
(3)根据抽样调查的结果,请你估计该校1500名学生中有多少名学生最喜欢踢毽子?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=10,BC=15,tan∠A=![]() 点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
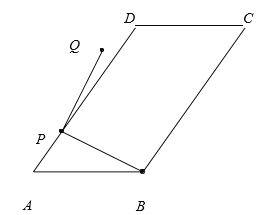
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
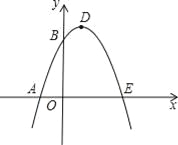
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)探究:
问题:如图1,等边三角形ABC的边长为6,点O是∠ABC和∠ACB的角平分线交点,∠FOG=120°,绕点O任意旋转∠FOG,分别交△ABC的两边于D,E两点求四边形ODBE的面积.
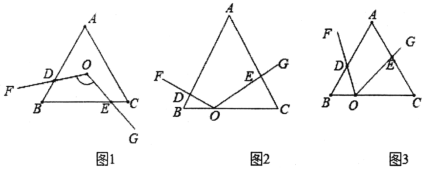
讨论:
①甲:在∠FOG旋转过程中,当OF经过点B时,OG一定经过点C.
②乙:小明的分析有道理,这样,我们就可以利用“ASA”证出△ODB≌△OEC.
③丙:因为△ODB≌△OEC,所以只要算出△OBC的面积就得出了四边形ODBE的面积.
老师:同学们的思路很清晰,也很正确,在分析和解决问题时,我们经常会借用特例作辅助线来解决一般问题请你按照探究的思路,直接写出四边形ODBE的面积:________.
(2)应用:
①特例:如图2,∠FOG的顶点O在等边三角形ABC的边BC上,OB=2,OC=4,边OG⊥AC于点E,OF⊥AB于点D,求△BOD面积.
②探究:如图3,已知∠FOG=60°,顶点O在等边三角形ABC的边BC上,OB=2,OC=4,记△BOD的面积为x,△COE的面积为y,求xy的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】一次函数y=kx+b的图象与反比例函数![]() 的图象交于点A(-2,-5),C(n,2),交y轴于点B,交x轴于点D.
的图象交于点A(-2,-5),C(n,2),交y轴于点B,交x轴于点D.
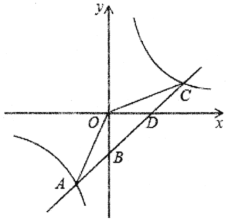
(1)求反比例函数![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)请直接写出不等式![]() 的解集.
的解集.
(3)连接OA,OC.求△AOC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.

(1)判断AF和⊙O的位置关系并说明理由.
(2)若∠ABC=60°,BC=1cm,求阴影部分的面积.(结果保留根号).
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D四个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
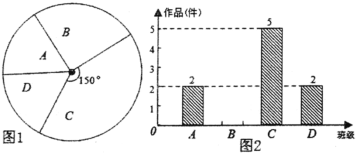
(1)李老师采取的调查方式是______________(填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共_________件,其中B班征集到作品_______________件.
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要抽取两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程).
查看答案和解析>>
科目: 来源: 题型:
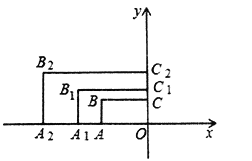
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B2,以此类推,得到的矩形A2020OC2020B2020的对角线交点的纵坐标为______________.
倍,得到矩形A2OC2B2,以此类推,得到的矩形A2020OC2020B2020的对角线交点的纵坐标为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com