
科目: 来源: 题型:
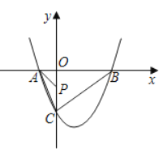
【题目】如图,已知二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,其中
,其中![]() .
.
(1)求点![]() 的坐标,并用含
的坐标,并用含![]() 的式子表示
的式子表示![]() ;
;
(2)连接![]() ,
,![]() ,当
,当![]() 为锐角时,求
为锐角时,求![]() 的取值范围;
的取值范围;
(3)若![]() 为
为![]() 轴上一个动点,连接
轴上一个动点,连接![]() ,当点
,当点![]() 的坐标为
的坐标为![]() 时,直接写出
时,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】复课返校后,为了拉大学生锻炼的间距,学校决定增购适合独立训练的两种体育器材:跳绳和毽子.如果购进5根跳绳和6个毽子共需196元;购进2根跳绳和5个键子共需120元.
(1)求一根跳绳和一个毽子的售价分别是多少元;
(2)学校计划购买跳绳和键子两种器材共400个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于310根,请你求出学校花钱最少的购买方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】复课返校后,为了让同学们进一步了解“新型冠状病毒”的防控知识,某学校组织了一次关于“新型冠状病毒”的防控知识比赛,从问卷中随机抽查了一部分,对调查结果进行了分组统计,并制作了如下表格与条形统计图:
分组结果 | 频数 | 频率 |
A.完全掌握 | 30 | 0.3 |
B.比较清楚 | 50 |
|
C.不怎么清楚 |
| 0.15 |
D.不清楚 | 5 | 0.05 |
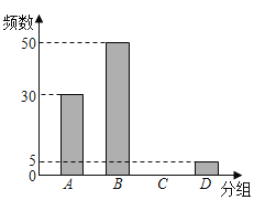
请根据上图完成下面题目:
(1)总人数为 人,![]() ,
,![]() ;
;
(2)请你补全条形统计图;
(3)若全校有2700人,请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少.
查看答案和解析>>
科目: 来源: 题型:
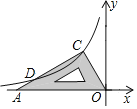
【题目】如图,把一块含30°角的三角板的直角顶点放在反比例函数y=-![]() (x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标为__________.
(x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的袋子里装有独立包装的口罩,其中粉色口罩有3个、蓝色口罩有2个,这些口罩除了颜色外全部相同,从中随机依次不放回拿出两个口罩,则两个口罩都是粉色的概率是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上,高
边上,高![]() 与正方形的边长相等,连接
与正方形的边长相等,连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,下列说法:①
,下列说法:①![]() ;②连接
;②连接![]() ,
,![]() ,则
,则![]() 为直角三角形;③
为直角三角形;③![]() ;④若
;④若![]() ,
,![]() ,则
,则![]() 的长为
的长为![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
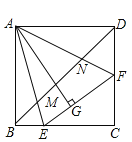
A.4B.3C.2D.1
查看答案和解析>>
科目: 来源: 题型:
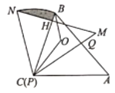
【题目】如图,两个三角形纸板![]() ,
,![]() 能完全重合,
能完全重合,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 从重合位置开始,按逆时针方向旋转,边
从重合位置开始,按逆时针方向旋转,边![]() ,
,![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合),点
重合),点![]() 是
是![]() 的内心,若
的内心,若![]() ,点
,点![]() 运动的路径为
运动的路径为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
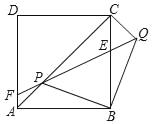
【题目】如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.
(1)求该抛物线的函数解析式;
(2)已知直线![]() 的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线![]() 于点H,连结OP,试求△OPH的面积;
于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线![]() 的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
的垂线,垂足为点E,F.是否在线段BC存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
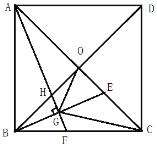
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(不与O、C重合),作AF⊥BE,垂足为G,分别交BC、OB于F、H,连接OG、CG.
(1)求证:AH=BE;
(2)∠AGO的度数是否为定值?说明理由;
(3)若∠OGC=90°,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com