
科目: 来源: 题型:
【题目】四边形ABCD的两条对角线AC、BD互相平分.添加下列条件,一定能判定四边形ABCD为菱形的是( )
A.∠ABD=∠BDCB.∠ABD=∠BACC.∠ABD=∠CBDD.∠ABD=∠BCA
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点![]() 与
与![]()
![]() 称为一对泛对称点.
称为一对泛对称点.
(1)若点![]() ,
,![]() 是一对泛对称点,求
是一对泛对称点,求![]() 的值;
的值;
(2)若![]() ,
,![]() 是第一象限的一对泛对称点,过点
是第一象限的一对泛对称点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,线段
,线段![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,判断直线
,判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)抛物线![]()
![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交此抛物线于点
轴的平行线交此抛物线于点![]() (不与点
(不与点![]() 重合),过点
重合),过点![]() 的直线
的直线![]() 与此抛物线交于另一点
与此抛物线交于另一点![]() .对于任意满足条件的实数
.对于任意满足条件的实数![]() ,是否都存在
,是否都存在![]() ,
,![]() 是一对泛对称点的情形?若是,请说明理由,并对所有的泛对称点
是一对泛对称点的情形?若是,请说明理由,并对所有的泛对称点![]() ,
,![]() 探究当
探究当![]() >
>![]() 时
时![]() 的取值范围;若不是,请说明理由.
的取值范围;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
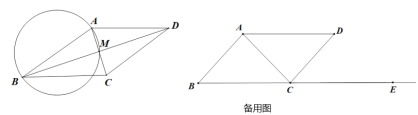
【题目】在![]() 中,
中,![]() 是锐角,过
是锐角,过![]() 两点以
两点以![]() 为半径作
为半径作![]()
(1)如图,对角线![]() 交于点
交于点![]() ,若
,若![]() ,且
,且![]() 过点
过点![]() ,求
,求![]() 的值
的值
(2)![]() 与边
与边![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 的长为
的长为![]() ,当
,当![]() 时,求
时,求![]() 的度数(提示:可再备用图上补全示意图)
的度数(提示:可再备用图上补全示意图)
查看答案和解析>>
科目: 来源: 题型:
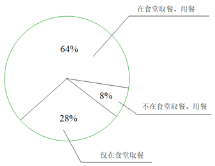
【题目】某公司有![]() 名职员,公司食堂供应午餐.受新冠肺炎疫情影响,公司停工了一段时间.为了做好复工后职员取餐、用餐的防疫工作,食堂进行了准备,主要如下:①将过去的自主选餐改为提供统一的套餐;②调查了全体职员复工后的午餐意向,结果如图
名职员,公司食堂供应午餐.受新冠肺炎疫情影响,公司停工了一段时间.为了做好复工后职员取餐、用餐的防疫工作,食堂进行了准备,主要如下:①将过去的自主选餐改为提供统一的套餐;②调查了全体职员复工后的午餐意向,结果如图![]() 所示;③设置不交叉的取餐区和用餐区,并将用餐区按一定的间距要求调整为可同时容纳
所示;③设置不交叉的取餐区和用餐区,并将用餐区按一定的间距要求调整为可同时容纳![]() 人用餐;④规定:排队取餐,要在食堂用餐的职员取餐后即进入用餐区用餐;⑤随机邀请了
人用餐;④规定:排队取餐,要在食堂用餐的职员取餐后即进入用餐区用餐;⑤随机邀请了![]() 名要在食堂取餐的职员进行了取餐、用餐的模拟演练,这
名要在食堂取餐的职员进行了取餐、用餐的模拟演练,这![]() 名职员取餐共用时
名职员取餐共用时![]() ,用餐时间(含用餐与回收餐具)如表所示.为节约时间,食堂决定将第一排用餐职员
,用餐时间(含用餐与回收餐具)如表所示.为节约时间,食堂决定将第一排用餐职员![]() 人的套餐先摆放在相应餐桌上,并在
人的套餐先摆放在相应餐桌上,并在![]() 开始用餐,其他职员则需自行取餐.
开始用餐,其他职员则需自行取餐.
用餐时间 | 人数 |
|
|
|
|
|
|
|
|
|
|
(1)食堂每天需要准备多少份午餐?
(2)食堂打算以参加演练的![]() 名职员用餐时间的平均数
名职员用餐时间的平均数![]() 为依据进行规划:前一批职员用餐
为依据进行规划:前一批职员用餐![]() 后,后一批在食堂用餐的职员开始取餐.为避免拥堵,需保证每位取餐后进入用餐区的职员都有座位用餐,则该规划是否可行?如果可行,请说明理由,并依此规划,根据调查统计的数据设计一个时间安排表,使得食堂不超过
后,后一批在食堂用餐的职员开始取餐.为避免拥堵,需保证每位取餐后进入用餐区的职员都有座位用餐,则该规划是否可行?如果可行,请说明理由,并依此规划,根据调查统计的数据设计一个时间安排表,使得食堂不超过![]() 就可结束取餐、用餐服务,开始消杀工作;如果不可行,也请说明理由.
就可结束取餐、用餐服务,开始消杀工作;如果不可行,也请说明理由.
查看答案和解析>>
科目: 来源: 题型:
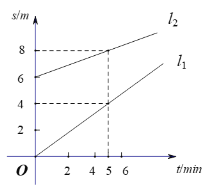
【题目】探测气球甲从海拔![]() 处出发,与此同时,探测气球乙从海拔
处出发,与此同时,探测气球乙从海拔![]() 处出发.图中的
处出发.图中的![]() 分别表示甲、乙两个气球所在位置的海拔
分别表示甲、乙两个气球所在位置的海拔![]() (单位:
(单位:![]() )与上升时间
)与上升时间![]() (单位:
(单位:![]() )之间的关系.
)之间的关系.
(1)求![]() 的函数解析式;
的函数解析式;
(2)探测气球甲从出发点上升到海拔![]() 处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
处的过程中,是否存在某一时刻使得探测气球甲、乙位于同一高度?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是某品牌台灯竖直摆放在水平桌面上的侧面示意图,其中![]() 为桌面(台灯底座的厚度忽略不计),台灯支架
为桌面(台灯底座的厚度忽略不计),台灯支架![]() 与灯管
与灯管![]() 的长度都为
的长度都为![]() ,且夹角为
,且夹角为![]() (即
(即![]() ),若保持该夹角不变,当支架
),若保持该夹角不变,当支架![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 时,支架与灯管落在
时,支架与灯管落在![]() 位置(如图2所示),则灯管末梢
位置(如图2所示),则灯管末梢![]() 的高度会降低_______
的高度会降低_______![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某二次函数的图象是一条顶点为P(4.-4)的抛物线,它经过原点和点A,它的对称轴交线段
OA于点M.点N在对移轴上,且点M、N关于点P对称,连接AN,ON
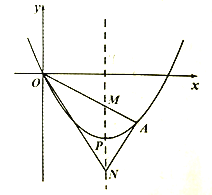
(1)求此二次函数的解析式:
(2)若点A的坐标是(6,-3).,请直接写出MN的长
(3)若点A在抛物线的对称轴右侧运动时,则∠ANM与∠ONM有什么数量关系?并证明.
查看答案和解析>>
科目: 来源: 题型:
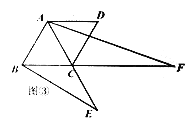
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE连接BE

(1)发现问题:如图①,若E是线段AC的中点,连接EF,其他条件不变,猜想线段BE与EF的数量关系
(2)探究问题:如图②,若E是线段AC上任意一点,连接EF,其他条件不变,猜想线段BE与EF的数量关系是什么?请证明你的猜想
(3)解决问题:如图③,若E是线段AC延长线上任意一点,其他条件不变,且∠EBC=30°,AB=3请直接写出AF的长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com