A.平均数B.众数C.中位数D.方差

【题目】如图，在平面直角坐标系中，直线分别与x、y轴交于A、B两点，将直线AB沿着y轴翻折，交x轴负半轴于点C．

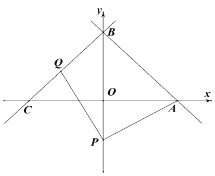
（1）求直线BC的函数关系式；

（2）点P（0，t）在y轴负半轴上，Q为线段BC上一动点（不与B、C重合）．连接PA、PQ，PQ＝PA

①若点Q为BC中点，求t的值；

②用t的代数式表示点Q的坐标和直线PQ的函数关系式；

③若M（2m，n－8），N（t3＋2t2－2m，n）在直线PQ上，求n的取值范围．

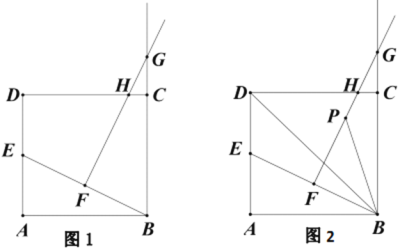
（1）连接HE、HB

①求证：HE＝HB；

②若a＝4，求CH的长．

（2）连接EG，△BEG面积为S

①BE＝ （用含a的代数式表示）；

②求S与a的函数关系式．

（3）如图2，设FG的中点为P，连接PB、BD．猜想∠GBP与∠DBE的关系，并说明理由．

【题目】如图，抛物线过A（－1，0）、B（3，0），直线AD交抛物线于点D，点D的横坐标为2，点P（m，n）是线段AD上的动点．

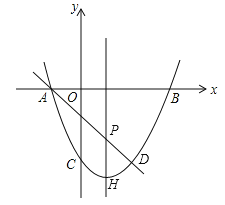
（1）求抛物线和直线AD的解析式；

（2）过点P的直线垂直于x轴，交抛物线于点H，

①求线段PH的长度l与m的关系式；

②当PH＝2时，求点P的坐标．

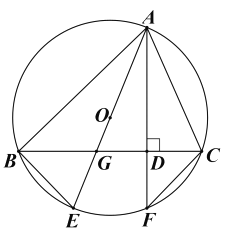
（1）求证：∠BAE＝∠CAF；

（2）若AB＝8，AC＝6，AG＝5，求AF的长．

【题目】如图，点A（2，m），B（－2，3m）分别在反比例函数和 的图象上，经过点A、B的直线与y轴相交于点C．

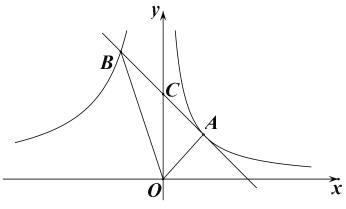
（1）求m和k的值；

（2）求△AOB的面积．

（1）小明同学的两次练习成绩之和为260分，综合成绩为132分，则他这两次练习成绩各得多少分？

（2）如果小张同学第一次练习成绩为120分，综合成绩要达到优秀，他的第二次练习成绩至少要得多少分？

（1）随机摸出一个球是黑球的概率为 ；若先从袋子里取出m个红球（不放回），再从袋子里随机摸出一个球，将“摸到黑球”记为事件A．若事件A为必然事件，则m＝ ；

（2）若从袋子里一次摸出两个球，用列表法或画树状图法列出所有等可能结果，并求摸出的两球颜色不同的概率．

（1）这10位居民一周内使用共享单车次数的中位数是 次，众数是 次．

（2）若小明同学把数据“20”看成了“30”，那么中位数，众数和平均数中不受影响的是 ．（填“中位数”，“众数”或“平均数”）

（3）若该小区有2000名居民，试估计该小区居民一周内使用共享单车的总次数．