
科目: 来源: 题型:
【题目】如图,点A在反比例函数y=![]() (x>0)的图像上,点B在反比例函数y=
(x>0)的图像上,点B在反比例函数y=![]() (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
(x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
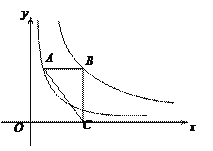
A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=![]() x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求证:AP∥BC;
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
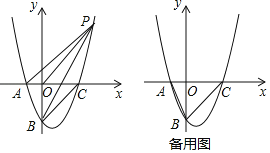
查看答案和解析>>
科目: 来源: 题型:
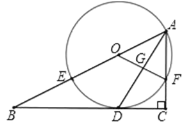
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)求证:![]() ;
;
(3)若BE=8,sinB=![]() ,求AD的长,
,求AD的长,
查看答案和解析>>
科目: 来源: 题型:
【题目】俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.
(1)求甲、乙两种品牌的足球的单价各是多少元?
(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目: 来源: 题型:
【题目】王老师为了解同学们对金庸武侠小说的阅读情况,随机对初三年级的部分同学进行调查,将调查结果分成以下五类:A:看过0~3本,B:看过4~6本,C:看过7~9本,D:看过10~12本,E:看过13~15本.并根据调查结果绘制了如图1、图2两幅不完整的统计图.
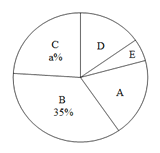
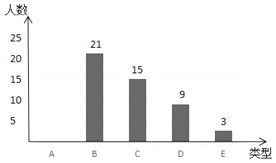
(1)图2中的a = ,D所对的圆心角度数为 °;
(2)请补全条形统计图;
(3)本次调查中E类有2男1女,王老师想从中抽取2名同学分别撰写一篇读书笔记.请用列表或画树状图的方法求所抽取的两名学生恰好是一男一女的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,CE是□ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E、连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )个.
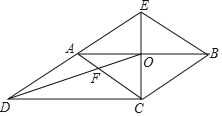
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB是半圆O的直径,AB=6,点C在半圆O上.过点A作AD⊥OC,垂足为点D,AD的延长线与弦BC交于点E,与半圆O交于点F(点F不与点B重合).
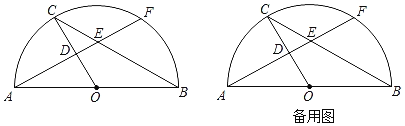
(1)当点F为![]() 的中点时,求弦BC的长;
的中点时,求弦BC的长;
(2)设OD=x,![]() =y,求y与x的函数关系式;
=y,求y与x的函数关系式;
(3)当△AOD与△CDE相似时,求线段OD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2﹣4ax+3的图象与x轴正半轴交于点A、B,与y轴相交于点C,顶点为D,且tan∠CAO=3.
(1)求这个二次函数的解析式;
(2)点P是对称轴右侧抛物线上的点,联结CP,交对称轴于点F,当S△CDF:S△FDP=2:3时,求点P的坐标;
(3)在(2)的条件下,将△PCD沿直线MN翻折,当点P恰好与点O重合时,折痕MN交x轴于点M,交y轴于点N,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com