
科目: 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
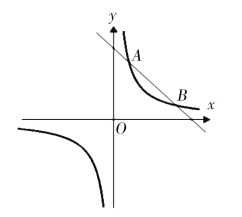
【题目】如图,双曲线![]() 与直线
与直线![]() 相交于
相交于![]() ,点P是x轴上一动点.
,点P是x轴上一动点.
(1)求双曲线![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)当![]() 时,直接写出x的取值范围;
时,直接写出x的取值范围;
(3)当![]() 是等腰三角形时,求点P的坐标.
是等腰三角形时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
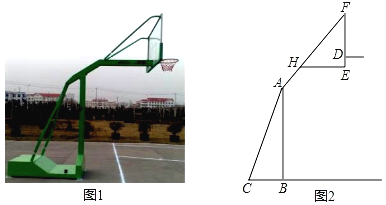
【题目】如图1、图2是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮筐D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮筐D到地面的距离.(精确到0.1米,参考数据:cos75°≈0.3,sin75°≈0.9,tan75°≈3.7,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目: 来源: 题型:
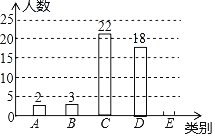
【题目】某校响应国家号召,鼓励学生积极参与体育锻炼.为了解学生一星期参与体育锻炼的时间情况,从全校2000名学生中,随机抽取50名学生进行调查,按参与体育锻炼的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
(1)样本中E类学生有 人,补全条形统计图;
(2)估计全校的D类学生有 人;
(3)从该样本参与体育锻炼时间在0≤t≤4的学生中任选2人,求这2人参与体育锻炼时间都在2<t≤4中的概率.
查看答案和解析>>
科目: 来源: 题型:
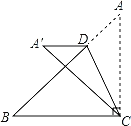
【题目】如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,ABCD为平行四边形,AD=13,AB=25,∠DAB=α,且cosa=![]() ,点E为直线CD上一动点,将线段EA绕点E逆时针旋转α得到线段EF,连接CF.
,点E为直线CD上一动点,将线段EA绕点E逆时针旋转α得到线段EF,连接CF.
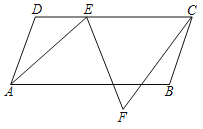
(1)求平行四边形ABCD的面积;
(2)当点C、B、F三点共线时,设EF与AB相交于点G,求线段BG的长;
(3)求线段CF的长度的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线G:y=x2-2mx与直线l:y=3x+b相交于A,B两点(点A的横坐标小于点B的横坐标)
(1)求抛物线y=x2-2mx顶点的坐标(用含m的式子表示);
(2)已知点C(-2,1),若直线l经过抛物线G的顶点,求△ABC面积的最小值;
(3)若平移直线l,可以使A,B两点都落在x轴的下方,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC=![]() ,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
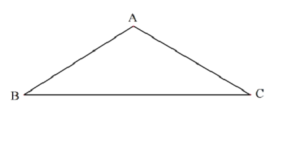
(1)求作圆O(尺规作图,保留作留痕迹,不写作法);
(2)求证:AC是OO的切线;
(3)若点P为圆O上一点,且弧PA=弧PB,连接PC,求线段PC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,一次函数y=k1x+8的图像与坐标轴分别相较于点A,B与反比例y=![]() 函数的图像相交于C,D.过点C作CE⊥y轴,垂足为E.且CE=2.
函数的图像相交于C,D.过点C作CE⊥y轴,垂足为E.且CE=2.
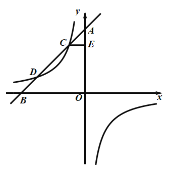
(1)求4k1-k2的值;
(2)若CD=2AC,求反比例函数的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】疫情期间为了满足口罩需求,某学校决定购进A,B两种型号的口罩.若购进A型口罩10盒,B型口罩5盒,共需1000元:若购进4型口罩4盒,B型口罩3盒,共需550元,(1)求A,B两种型号的口罩每盒各需多少元?
(2)若该学校决定购进这两种型号的口罩共计200盒,考虑到实际需求,要求购进A型号口罩的盒数不超过B型口罩盒数的6倍,请为该学校设计出最省钱的方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com