
科目: 来源: 题型:
【题目】如图,在□ABCD中,点E、F分别在边CD、AB上,且满足CE=AF.
(1)求证:△ADE≌△CBF;
(2)连接AC,若AC恰好平分∠EAF,试判断四边形AECF为何种特殊的四边形?并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.﹣1≤t≤0B.﹣1≤t![]() C.
C.![]() D.t≤﹣1或t≥0
D.t≤﹣1或t≥0
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A. 一组数据2,2,3,4,这组数据的中位数是2
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分
D. 某日最高气温是![]() ,最低气温是
,最低气温是![]() ,则该日气温的极差是
,则该日气温的极差是![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长.
(2)求经过O,D,C三点的抛物线的解析式.
(3)一动点P从点C出发,沿CB以每秒2个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ.
(4)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,直接写出M点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
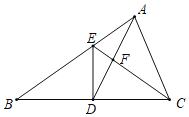
【题目】如图,在△ABC中,AD是BC边上的中线,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)过点A作AM⊥BC于点M,求DE:AM的值;
(3)若S△FCD=5,BC=10,求DE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的口袋中装有4张卡片,卡片上分別标有数字1、﹣2、3、﹣4,这些卡片除数字外都相同.王兴从口袋中随机抽取一张卡片,钟华从剩余的三张卡片中随机抽取一张,求两张卡片上数字之积.
(1)请你用画树状图或列表的方法,列出两人抽到的数字之积所有可能的结果.
(2)求两人抽到的数字之积为正数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】(12分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.
(1)若商场平均每天要盈利1600元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
查看答案和解析>>
科目: 来源: 题型:
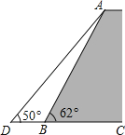
【题目】如图,某防洪堤坝长300米,其背水坡的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得加固后坡面的坡角∠ADB=50°
(1)求此时应将坝底向外拓宽多少米?(结果保留到0.01米)
(2)完成这项工程需要土石多少立方米?(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com