
科目: 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,E,F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确都有( )个.
①QB=QF;②AE⊥BF;③![]() ;④
;④![]() ;④S四边形ECFG=2S△BGE
;④S四边形ECFG=2S△BGE

A.5B.4C.3D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形纸片ABCD中,AD∥BC,∠B=90°,BC=CD=6, ∠C=60°.点E是边AD上一点,连接BE,将△ABE沿BE翻折得到△HBE .
(1)当点B、D、H三点在一直线上时,求线段AE的长;
(2)当点A的对称点H正好落在DC上时,有动点P从点H出发沿线段HB向点B运动,同时动点Q从点B出发沿线段BA向点A运动,速度均为每秒1个单位长度,连接PQ交折痕BE于点M.设运动时间为t秒.
① 探究:当时间t为何值时,△PBM为等腰三角形;
② 连接AM,请直接写出BM+2AM的最小值是 .

查看答案和解析>>
科目: 来源: 题型:
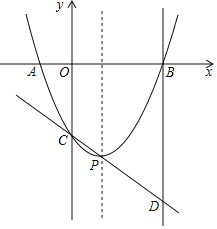
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,顶点为P,直线
轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,顶点为P,直线![]() 与过点B且垂直于
与过点B且垂直于![]() 轴的直线交于点D,且CP:PD=1:2,tan∠PDB=
轴的直线交于点D,且CP:PD=1:2,tan∠PDB=![]() .
.
(1)请直接写出A、B两点的坐标:A , B ;
(2)求这个二次函数的解析式;
(3)在抛物线的对称轴上找一点M使|MC-MB|的值最大,则点M的坐标为____.
查看答案和解析>>
科目: 来源: 题型:
【题目】水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的部分数据如下表:
销售时间t(1≤t≤15,t为整数)(天) | 1 | 4 | 5 | 8 | 12 |
销售单价p(元/千克) | 20.25 | 21 | 21.25 | 22 | 23 |
已知p与t之间的变化规律符合一次函数关系.
(1)试求p关于t的函数表达式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=-2t+120(1≤t≤15,t为整数).
① 求销售过程中最大日销售利润为多少?
② 在实际销售的前12天中,公司决定每销售1千克水果就捐赠n元利润(n<3)给“精准扶贫”对象.现发现:在前12天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,DM切⊙O于点D,过点A作AE⊥DM,垂足为E,交⊙O于点C,连接AD.
(1)求证:AD是∠BAC的平分线;
(2)连接CD,若![]() ,半径为5,求CE的长.
,半径为5,求CE的长.
![]()

查看答案和解析>>
科目: 来源: 题型:
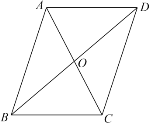
【题目】在一次数学活动中,老师准备三张完全相同的纸片,纸片上分别写有如图所示图形的一个条件:①AD=BC;②AB∥DC;③AO=OC,小明同学从三张纸片中任意抽取两张.请你用树状图或表格表示出抽取两张纸片上的条件所有可能出现的结果(用序号表示),并求出上述条件下四边形ABCD是平行四边形的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
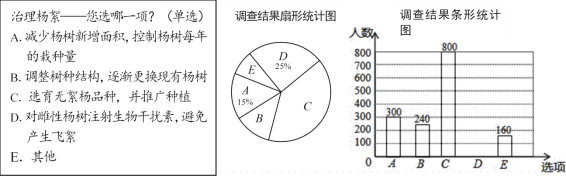
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 °;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目: 来源: 题型:
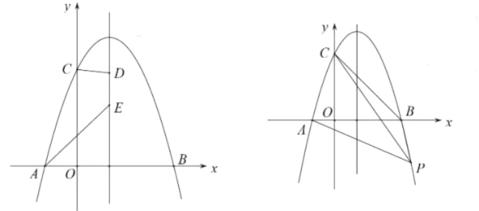
【题目】如图所示抛物线![]() 过点
过点![]() ,点
,点![]() ,且
,且![]()
(1)求抛物线的解析式及其对称轴;
(2)点![]() 在直线
在直线![]() 上的两个动点,且
上的两个动点,且![]() ,点
,点![]() 在点
在点![]() 的上方,求四边形
的上方,求四边形![]() 的周长的最小值;
的周长的最小值;
(3)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为3∶5两部分,求点
的面积分为3∶5两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
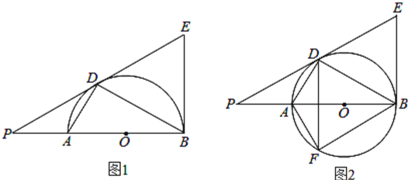
【题目】如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E.
(1)证明:直线PD是⊙O的切线;
(2)如果∠BED=60°,PD=![]() ,求PA的长;
,求PA的长;
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com