
科目: 来源: 题型:
【题目】为进一步推动各级各类学校新型冠状病毒肺炎疫情防控工作,向广大教职工和学生普及新型冠状病毒肺炎疫情防控知识,做好师生返校前的卫生安全防护教育,上好开学第一课,省教育厅要求各级各类学校认真学习相关资料.某中学为了解学生的学习成果,对学生进行了新型冠状病毒肺炎防控知识测试,德育处随机从七、八两个年级各抽取20名学生的答卷成绩(单位:分)进行统计分析,过程如下:
收集数据
八年级:
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
七年级:
80 | 60 | 80 | 95 | 65 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
整理数据
成绩 |
|
|
|
|
八年级 | 2 | 5 |
|
|
七年级 | 3 | 7 | 5 | 5 |
分析数据
统计量 | 平均数 | 中位数 | 众数 |
八年级 | 85.75 | 87.5 |
|
七年级 | 83.5 |
| 80 |
应用数据
(1)填空:![]() __________,
__________,![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)看完统计数据,你认为对新型冠状病毒肺炎防护知识掌握更好的年级是__________;
(3)若八年级共有500人参与答卷,请估计八年级成绩大于90分的人数;
(4)在这次测试中,八年级学生甲与七年级学生乙的成绩都是85分,请判断两人在各自年级的排名谁更靠前,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 为AC边中点,动点
为AC边中点,动点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路径以每秒1个单位长度的速度运动到
的路径以每秒1个单位长度的速度运动到![]() 点,在此过程中线段
点,在此过程中线段![]() 的长度
的长度![]() 随着运动时间
随着运动时间![]() 变化的函数关系如图2所示,则边
变化的函数关系如图2所示,则边![]() 的长为__________.
的长为__________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A(![]() ,4),B(3,m)是直线AB与反比例函数
,4),B(3,m)是直线AB与反比例函数![]() (x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
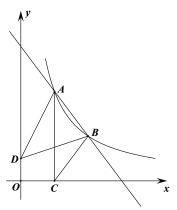
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2,求S2-S1.
查看答案和解析>>
科目: 来源: 题型:
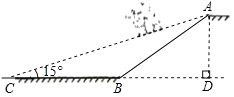
【题目】若商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,扶梯AB的坡度i为1:![]() .改造后的斜坡式动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度.
.改造后的斜坡式动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度.
(结果精确到0.1m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
查看答案和解析>>
科目: 来源: 题型:
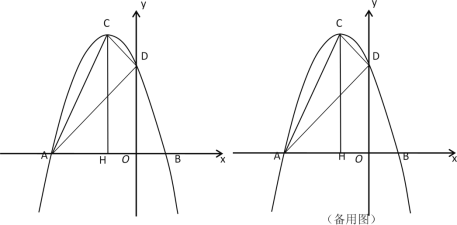
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
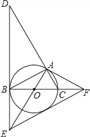
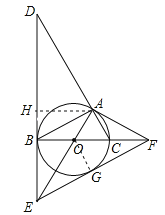
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC=![]() ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.
【答案】(1) 见解析; (2)3![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)根据圆周角定理得到∠BAC=90°,根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°,∠DBC=90°,于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论;
(2)根据S△AOC=![]() ,得到S△ACF=
,得到S△ACF=![]() ,通过△ACF∽△DAE,求得S△DAE=
,通过△ACF∽△DAE,求得S△DAE=![]() ,过A作AH⊥DE于H,解直角三角形得到AH=
,过A作AH⊥DE于H,解直角三角形得到AH=![]() DH=
DH=![]() DE,由三角形的面积公式列方程即可得到结论;
DE,由三角形的面积公式列方程即可得到结论;
(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG=![]() (180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
(180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
试题解析:(1)证明:∵BC是⊙O的直径,∴∠BAC=90°,∵∠ABC=30°,∴∠ACB=60°
∵OA=OC,∴∠AOC=60°,∵AF是⊙O的切线,∴∠OAF=90°,∴∠AFC=30°,∵DE是⊙O的切线,∴∠DBC=90°,∴∠D=∠AFC=30,∵∠DAE=ACF=120°,∴△ACF∽△DAE;
(2)∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°,∴∠CAF=30°,∴∠CAF=∠AFC,∴AC=CF,∴OC=CF,∵S△AOC=![]() ,∴S△ACF=
,∴S△ACF=![]() ,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=
,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=![]() BD,∴AF=
BD,∴AF=![]() BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴
BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴![]() ,∵△ACF∽△DAE,∴
,∵△ACF∽△DAE,∴![]() =
=![]() ,∴S△DAE=
,∴S△DAE=![]() ,过A作AH⊥DE于H,∴AH=
,过A作AH⊥DE于H,∴AH=![]() DH=
DH=![]() DE,∴S△ADE=
DE,∴S△ADE=![]() DEAH=
DEAH=![]() ×
×![]()
![]() =
=![]() ,∴DE=
,∴DE=![]() ;
;
(3)∵∠EOF=∠AOB=120°,∴∠OEB=∠AFO,在△AOF与△BOE中,∵∠OBE=∠OAF,∠OEB=∠AFO,OA=OB,∴△AOF≌△BEO,∴OE=OF,∴∠OFG=![]() (180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
(180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
【题型】解答题
【结束】
25
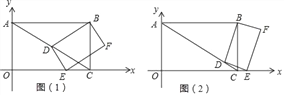
【题目】如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2![]() ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
(1)填空:点B的坐标为 ;
(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;
(3)①求证:![]() ;
;
②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.
查看答案和解析>>
科目: 来源: 题型:
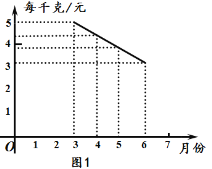
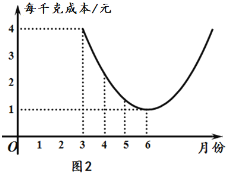
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示.
(1)已知6月份这种蔬菜的成本最低,此时出售每干克的收益是多少元?(收益=售价-成本)
(2)分别求出y1、y2与x之间的函数关系式;
(3)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com