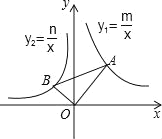
【题目】如图，在平面直角坐标系中，∠AOB＝90°，∠OAB＝30°，反比例函数y1＝的图象经过点A，反比例函数y2＝的图象经过点B，则下列关于m，n的关系正确的是（　　）

A.m＝nB.m＝﹣nC.m＝﹣nD.m＝﹣3n

【题目】如果一个四边形的对角线把四边形分成两个三角形，一个是等边三角形，另一个是该对角线所对的角为的三角形，我们把这条对角线叫做这个四边形的理想对角线，这个四边形称为理想四边形．

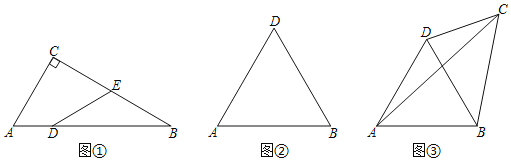
（1）如图①，在中，，，，为上一点，，为中点，连接，求证：四边形为理想四边形；

（2）如图②，是等边三角形，若为理想对角线，四边形为理想四边形．请画图找出符合条件的C点落在怎样的图形上；(在图中标出必要的数据)

（3）在（2）的条件下，

①若为直角三角形，，求的长度；

②如图③，若，，，请直接写出、、之间的数量关系．

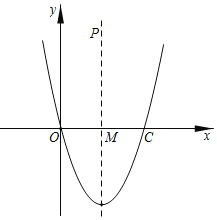
【题目】已知抛物线顶点坐标为，且与轴交于原点和点．对称轴与轴交点为．

（1）求抛物线的解析式；

（2）若点在抛物线上，且横坐标为，在抛物线对称轴上找一点，使得与的差最大，求此时点的坐标；

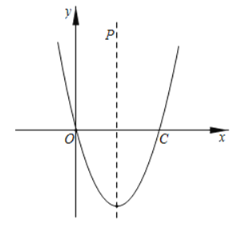
（3）若点在抛物线的对称轴上，且纵坐标为．探究：在抛物线上是否存在点使得四点共圆？若存在求出点坐标；若不存在请说明理由．

对于两个正数a、b，则（当且仅当a＝b时取等号）．

当为定值时，有最小值；当为定值时，有最大值．

例如：已知，若，求的最小值．

解：由≥，得≥，当且仅当即时，有最小值，最小值为．

根据上面的阅读材料回答下列问题：

（1）已知，若，则当 　时，有最小值，最小值为 　；

（2）已知，若，则取何值时，有最小值，最小值是多少？

（3）用长为篱笆围一个长方形花园，问这个长方形花园的长、宽各为多少时，所围的长方形花园面积最大，最大面积是多少？

【题目】如图，内接于⊙，，∥交的延长线于点．

（1）求证：是⊙的切线；

（2）若，．

①求的度数；

②求的长．

【题目】年月日下午，由名队员组成的扬州市第七批支援湖北医疗队，肩负着国家的重托和神圣职责使命启程出征，其中小李、小王和三个同事共五人直接派往一线某医院，根据该院人事安排需要先抽出一人去重症监护，再派两人到发热门诊，请你利用所学知识完成下列问题．

（1）小李被派往重症监护的概率是 　；

（2）若正好抽出她们的一同事去往重症监护，请你利用画树状图或列表的方法，求出小李和小王同时被派往发热门诊的概率．

【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随杋抽取了名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：

学生最喜爱的节目人数统计表

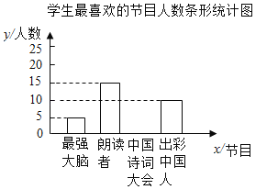
根据以上信息，回答下列问题：

（1） 　， 　；

（2）补全上面的条形统计图；

（3）若该校共有学生名，估计该校学生最喜爱《朗读者》节目的人数．

【题目】已知在平面直角坐标系中，点的坐标为，是第一象限内任意一点，连接 、，若，，则就叫做点的“双角坐标”．例如：点的“双角坐标”为．若点到轴的距离为，则的最小值为___．

【题目】抛物线与轴交于A，B两点，与轴交于点C，连接BC．

（1）如图1，求直线BC的表达式；

（2）如图1，点P是抛物线上位于第一象限内的一点，连接PC，PB，当△PCB面积最大时，一动点Q从点P从出发，沿适当路径运动到轴上的某个点G处，再沿适当路径运动到轴上的某个点H处，最后到达线段BC的中点F处停止，求当△PCB面积最大时，点P的坐标及点Q在整个运动过程中经过的最短路径的长；

（3）如图2，在（2）的条件下，当△PCB面积最大时，把抛物线向右平移使它的图象经过点P，得到新抛物线，在新抛物线上，是否存在点E，使△ECB的面积等于△PCB的面积．若存在，请求出点E的坐标，若不存在，请说明理由．