
科目: 来源: 题型:
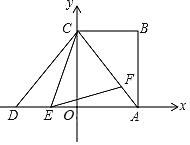
【题目】如图,矩形ABCD的顶点A、C在平面直角坐标系的坐标轴上,AB=4,CB=3,点D与点A关于y轴对称,点E、F分别是线段DA、AC上的动点(点E不与A、D重合),且∠CEF=∠ACB,若△EFC为等腰三角形,则点E的坐标为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+4![]() ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+![]() ,其中正确的结论是( )
,其中正确的结论是( )

A. ①②③⑤ B. ①②③④ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目: 来源: 题型:
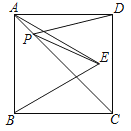
【题目】如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形内,在对角线AC上找到一点P,使PD+PE的和最小,则这个和的最小值是( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目: 来源: 题型:
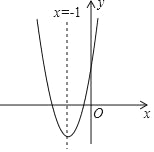
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1.有下列结论:①b2=4ac ②abc>0 ③a>c ④4a+c>2b.其中结论正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
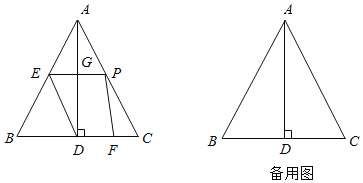
【题目】已知:如图,在等边△ABC中,AB=6cm,AD⊥BC于点D,动点F从点C出发,沿CB方向以1cm/s的速度向点D运动;同时,动点P也从点C出发,沿CA方向以3cm/s的速度向点A运动,过点P作PE∥BC,与边AB交于点E,与AD交于点G,连结ED,PF.设运动的时间为t(s)(0<t<2).
(1)当t为何值时,四边形EDFP为平行四边形?
(2)设四边形EDFP面积为y,求y与t之间的函数关系式;
(3)连结PD、EF,当t为何值时,PD⊥EF?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔,纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:
loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:logaM=m,logaN=n,则M=am,N=an
∴MN=aman=am+n,由对数的定义得m+n=loga(MN)
又∵m+n=logaM+logaN
∴loga(MN)=logaM+logaN
解决以下问题:
(1)将指数式53=125转化为对数式 ;
(2)log24= ,log381= ,log464= .(直接写出结果)
(3)证明:证明loga![]() =logaM﹣logaN(a>0,a≠1,M>0,N>0).(写出证明过程)
=logaM﹣logaN(a>0,a≠1,M>0,N>0).(写出证明过程)
(4)拓展运用:计算计算log34+log312﹣log316= .(直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,点G,H在对角线BD上,且BG=DH.
(1)求证:△BFH≌△DEG;
(2)连接DF,若DF=BF,则四边形EGFH是什么特殊四边形?证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
【题目】某中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜,若购买8个A型放大镜和5个B型放大镜需用440元;若购买4个A型放大镜和6个B型放大镜需用304元.
(1)求每个A型放大镜和每个B型放大镜各多少元?
(2)该中学决定购买A型和B型放大镜共75个,总费用不超过2360元,则最多可以购买多少个A型放大镜?
查看答案和解析>>
科目: 来源: 题型:
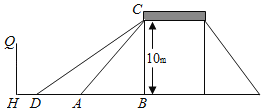
【题目】如图,是一座人行天桥示意图,天桥离地面的高BC是10m,坡面AC的倾斜角∠CAB=45°,在距离A点12m处有一建筑物HQ.为方便行人过天桥,市政部门决定降低坡度,使新坡面CD的倾斜角∠CDB=37°,若新坡面下D处需留至少4m人行道,则该建筑物HQ是否需要拆除?请通过计算说明理由.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】小明与小亮玩游戏,如图,两组相同的纸牌,每组三张,牌面数字分别是3,4,5.他们将卡片背面朝上,分组充分洗匀后,从每组纸牌中各摸出一张,称为一次游戏.当摸出的两张纸牌的牌面数字之和大于8,则小明获胜;当摸出的两张纸牌的牌面数字之和小于8,则小亮获胜.
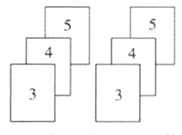
(1)请你用列表法或画树状图法求出小明获胜的概率;
(2)这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com