
科目: 来源: 题型:
【题目】如图所示,E是矩形ABCD的边BC上一点,EF⊥AE,分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
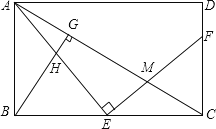
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=4,求EM的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】下图1是儿童写字支架示意图,由一面黑板,一面白板和一块固定支架的托盘组成,图2是它的一个左侧截面图,该支架是个轴对称图形,∠BAC是可以转动的角,B,C、D,E和F,G是支架腰上的三对对称点,是用来卡住托盘以固定支架的。已知AB=AC=60cm,BD=CE=DF=EG=10cm。
(1)当托盘固定在BC处时,∠BAC=32,求托盘BC的长;(精确到0.1)
(2)当托盘固定在DE处时,这是儿童看支架的最佳角度,求此时∠BAC的度数。
(参考数据:sin32=0.53,cos32=0.85,sin16=0.28
sin20=0.34,sin25=0.42。)


图1 图2
查看答案和解析>>
科目: 来源: 题型:
【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让学生进行摸球试验,每次摸出一个球(放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
|
(1)![]() = ,根据上表数据估计从袋中摸出一个黑球的概率是 .
= ,根据上表数据估计从袋中摸出一个黑球的概率是 .
(2)估算袋中白球的个数为 .
(3)在(2)的条件下,若小强同学从袋中摸出两个球,用画树状图或列表的方法计算摸出的两个球都是白球的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,现有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,在与墙平行的一边,开一扇2米宽的门.如果竹篱笆的长为33米,求这个长方形养鸡场与墙垂直的边长是多少?与墙平行的边长是多少?(列方程解答)

查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的方格中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
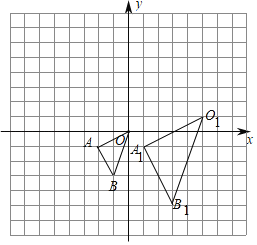
(1)在图中标出位似中心P的位置,并写出点P的坐标及△O1A1B1与△OAB的位似比;
(2)以原点O为位似中心,在y轴的左侧画出△OAB的另一个位似△OA2B2,使它与△OAB的位似比为2:1,并写出点B的对应点B2的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+![]() 与x轴分别交于点A(﹣1,0),B(3,0),点C是顶点.
与x轴分别交于点A(﹣1,0),B(3,0),点C是顶点.
(1)求抛物线的解析式;
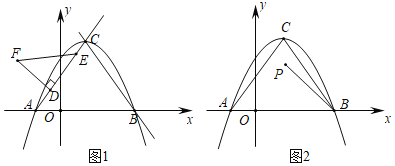
(2)如图1,线段DE是射线AC上的一条动线段(点D在点E的下方),且DE=2,点D从点A出发沿着射线AC的方向以每秒2个单位长度的速度运动,以DE为一边在AC上方作等腰Rt△DEF,其中∠EDF=90°,设运动时间为t秒.
①点D的坐标是 (用含t的代数式表示);
②当直线BC与△DEF有交点时,请求出t的取值范围;
(3)如图2,点P是△ABC内一动点,BP=![]() ,点M,N分别是AB,BC边上的两个动点,当△PMN的周长最小时,请直接写出四边形PNBM面积的最大值.
,点M,N分别是AB,BC边上的两个动点,当△PMN的周长最小时,请直接写出四边形PNBM面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】思维探索:
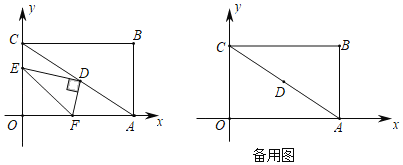
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 ;
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:
如图3,在Rt△ABC中,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC边OA,OC分别在x轴,y的正半轴上,且OA=8,OC=6,连接AC,点D为AC中点,点E从点C出发以每秒1个单位长度运动到点O停止,设运动时间为t秒(0<t<6),连接DE,作DF⊥DE交OA于点F,连接EF.
(1)当t的值为 时,四边形DEOF是矩形;
(2)用含t的代数式表示线段OF的长度,并说明理由;
(3)当△OEF面积为![]() 时,请直接写出直线DE的解析式.
时,请直接写出直线DE的解析式.
查看答案和解析>>
科目: 来源: 题型:
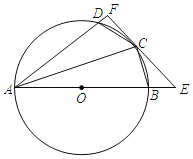
【题目】如图,四边形ABCD内接于⊙O,点O在AB上,BC=CD,过点C作⊙O的切线,分别交AB,AD的延长线于点E,F.
(1)求证:AF⊥EF;
(2)若cos∠DAB=![]() ,BE=1,则线段AD的长是_____.
,BE=1,则线段AD的长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com