
科目: 来源: 题型:
【题目】如图,已知△ABC,按如下步骤作图:
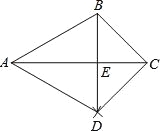
(1)以A圆心,AB长为半径画弧;
(2)以C为圆心,CB长为半径画弧,两弧相交于点D;
(3)连接BD,与AC交于点E,连接AD,CD.
①四边形ABCD是中心对称图形;
②△ABC≌△ADC;
③AC⊥BD且BE=DE;
④BD平分∠ABC.
其中正确的是( )
A.①② B.②③ C.①③ D.③④
查看答案和解析>>
科目: 来源: 题型:
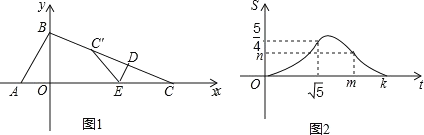
【题目】如图 1,直线 y=2x+2 分别交 x 轴、y 轴于点A、B,点C为x轴正半轴上的点,点 D从点C处出发,沿线段CB匀速运动至点 B 处停止,过点D作DE⊥BC,交x轴于点E,点 C′是点C关于直线DE的对称点,连接 EC′,若△ DEC′与△ BOC 的重叠部分面积为S,点D的运动时间为t(秒),S与 t 的函数图象如图 2 所示.
(1)VD ,C 坐标为 ;
(2)图2中,m= ,n= ,k= .
(3)求出S与t 之间的函数关系式(不必写自变量t的取值范围).
查看答案和解析>>
科目: 来源: 题型:
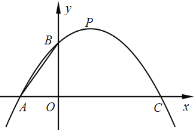
【题目】如图,二次函数![]() (a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(1)求 A、C 两点坐标;
(2)过点 B 作 BD∥x 轴交抛物线于 D,过点 P 作 PE∥AB 交 x 轴于 E,连接 DE,
①求 E 坐标;
②若 tan∠BPM=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
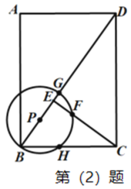
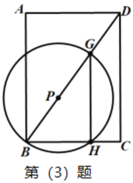
【题目】如图,在矩形 ABCD 中,CE⊥BD,AB=4,BC=3,P 为 BD 上一个动点,以 P 为圆心,PB 长半径作⊙P,⊙P 交 CE、BD、BC 交于 F、G、H(任意两点不重合),
(1)半径 BP 的长度范围为 ;
(2)连接 BF 并延长交 CD 于 K,若 tan KFC 3 ,求 BP;
(3)连接 GH,将劣弧 HG 沿着 HG 翻折交 BD 于点 M,试探究![]() 是否为定值,若是求出该值,若不是,请说明理由.
是否为定值,若是求出该值,若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
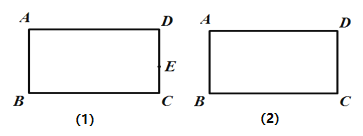
【题目】如图,四边形 ABCD 为矩形.
(1)如图1,E为CD上一定点,在AD上找一点F,使得矩形沿着EF折叠后,点D落在 BC边上(尺规作图,保留作图痕迹);
(2)如图2,在AD和CD边上分别找点M,N,使得矩形沿着MN折叠后BC的对应边B' C'恰好经过点D,且满足B' C' ⊥BD(尺规作图,保留作图痕迹);
(3)在(2)的条件下,若AB=2,BC=4,则CN= .
查看答案和解析>>
科目: 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目: 来源: 题型:
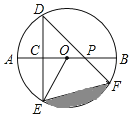
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
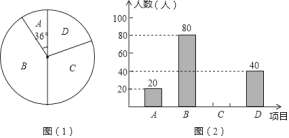
【题目】计划开设以下课外活动项目:A 一版画、B 一机器人、C 一航模、D 一园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生 必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;扇形统计图中,选“D一园艺种植”的学生人数所占圆心角的度数是 °;
(2)请你将条形统计图补充完整;
(3)若该校学生总数为 1500 人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总 人数
查看答案和解析>>
科目: 来源: 题型:
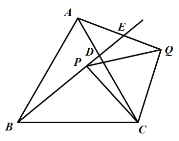
【题目】如图,在边长为 6 的等边△ABC 中,D 为 AC 上一点,AD=2,P 为 BD 上一点,连接 CP,以 CP 为 边,在 PC 的右侧作等边△CPQ,连接 AQ 交 BD 延长线于 E,当△CPQ 面积最小时,QE=____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com