
科目: 来源: 题型:
【题目】某市水果批发市场内有一种水果,保鲜期一周,如果冷藏,可以延长保鲜时间,但每天仍有一定数量的这种水果变质,假设这种水果保鲜期内的个体重量基本保持不变。现有一个体户,按市场价收购了这种水果200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后这种鲜水果每千克的价格每天可上涨0.2元,但存放一天需各种费用20元,日平均每天还有1千克变质丢弃.
(1)设![]() 天后每千克鲜水果的市场价
天后每千克鲜水果的市场价![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若存放![]() 天后将鲜水果一次性出售,设鲜水果的销售总金额为
天后将鲜水果一次性出售,设鲜水果的销售总金额为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)该个体户将这批水果存放多少天后出售,可获最大利润![]() ?最大利润
?最大利润![]() 是多少?
是多少?
(本题不要求写出自变量![]() 的取值范围)
的取值范围)
查看答案和解析>>
科目: 来源: 题型:
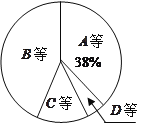
【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
D | 5分以下 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)试直接写出
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知平面直角坐标系,![]() 两点的坐标分别为
两点的坐标分别为![]() .
.

(1)若![]() 是
是![]() 轴上的一个动点,则当
轴上的一个动点,则当![]() _______时,
_______时,![]() 的周长最短;
的周长最短;
(2)若![]() 是
是![]() 轴上的两个动点,则当
轴上的两个动点,则当![]() _______时,四边形
_______时,四边形![]() 的周长最短;
的周长最短;
(3)设![]() 分别为
分别为![]() 轴和
轴和![]() 轴上的动点,请问:是否存在这样的点
轴上的动点,请问:是否存在这样的点![]() , 使四边形
, 使四边形![]() 的周长最短?若存在,请求出,
的周长最短?若存在,请求出,![]() _________,
_________,![]() ________(不必写解答过程);若不存在,请说明理由.
________(不必写解答过程);若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,现有一横截面是一抛物线的水渠.一次,水渠管理员将一根长![]() 的标杆一端放在水渠底部的
的标杆一端放在水渠底部的![]() 点,另一端露出水面并靠在水渠边缘的
点,另一端露出水面并靠在水渠边缘的![]() 点,发现标杆有
点,发现标杆有![]() 浸没在水中,露出水面部分的标杆与水面成
浸没在水中,露出水面部分的标杆与水面成![]() 的夹角(标杆与抛物线的横截面在同一平面内).
的夹角(标杆与抛物线的横截面在同一平面内).

(1)以水面所在直线为![]() 轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
(2)在(1)的条件下,求当水面再上升![]() 时的水面宽约为多少?(
时的水面宽约为多少?(![]() 取
取![]() ,结果精确到
,结果精确到![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是规格为![]() 的正方形网格,请在所给网格中按下列要求操作:
的正方形网格,请在所给网格中按下列要求操作:
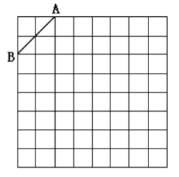
(1)请在网格中建立平面直角坐标系,使点![]() 坐标为
坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ;
;
(2)在第二象限内的格点上画一点![]() ,使点
,使点![]() 与线段
与线段![]() 组成一个以
组成一个以![]() 为底的等腰三角形,且腰长是无理数, 则
为底的等腰三角形,且腰长是无理数, 则![]() 点坐标是________,
点坐标是________,![]() 的周长是_________(结果保留根号);
的周长是_________(结果保留根号);
(3)画出![]() 以点
以点![]() 为旋转中心、旋转
为旋转中心、旋转![]() 后的
后的![]() ,连结
,连结![]() 和
和![]() ,试说出四边形
,试说出四边形![]() 是何特殊四边形, 并说明理由.
是何特殊四边形, 并说明理由.
查看答案和解析>>
科目: 来源: 题型:
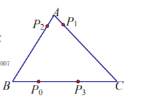
【题目】电子跳蚤游戏盘是如图所示的![]() ,
,![]() .如果跳蚤开始时在
.如果跳蚤开始时在![]() 边的
边的![]() 处,
处,![]() .跳蚤第一步从
.跳蚤第一步从![]() 跳到
跳到![]() 边的
边的![]() (第1次落点)处,且
(第1次落点)处,且![]() ;第二步从
;第二步从![]() 跳到
跳到![]() 边的
边的![]() (第2次落点)处,且
(第2次落点)处,且![]() ;第三步从
;第三步从![]() 跳到
跳到![]() 边的
边的![]() (第3次落点)处,且
(第3次落点)处,且![]() ;……;跳蚤按上述规则一直跳下去,第
;……;跳蚤按上述规则一直跳下去,第![]() 次落点为
次落点为![]() (
(![]() 为正整数),则点
为正整数),则点![]() 与
与![]() 之间的距离为( )
之间的距离为( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),点B(4,0),与y轴交于点C(0,8),连接BC,又已知位于y轴右侧且垂直于x轴的动直线l,沿x轴正方向从O运动到B(不含O点和B点),且分别交抛物线、线段BC以及x轴于点P,D,E.
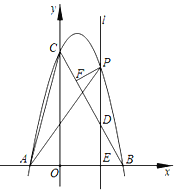
(1)求抛物线的表达式;
(2)连接AC,AP,当直线l运动时,求使得△PEA和△AOC相似的点P的坐标;
(3)作PF⊥BC,垂足为F,当直线l运动时,求Rt△PFD面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)阅读理解
如图,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,连接
的图象上,连接![]() ,取线段
,取线段![]() 的中点
的中点![]() .分别过点
.分别过点![]() ,
,![]() ,
,![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,![]() ,
,![]() ,
,![]() 交反比例函数
交反比例函数![]() 的图象于点
的图象于点![]() .点
.点![]() ,
,![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() ,
,![]() .小红通过观察反比例函数
.小红通过观察反比例函数![]() 的图象,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于
的图象,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于![]() ,
,![]() ,
,![]() 之间数量关系的命题:若
之间数量关系的命题:若![]() ,则______.
,则______.
(2)证明命题
小东认为:可以通过“若![]() ,则
,则![]() ”的思路证明上述命题.
”的思路证明上述命题.
小晴认为:可以通过“若![]() ,
,![]() ,且
,且![]() ,则
,则![]() ”的思路证明上述命题.
”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com