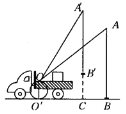
【题目】小刘同学在课外活动中观察吊车的工作过程，绘制了如图所示的平面图形．已知吊车吊臂的支点O距离地面的高度OO′=2米．当吊臂顶端由A点抬升至 A′点(吊臂长度不变)时，地面B处的重物(大小忽略不计)被吊至B′处，紧绷着的吊绳A′B′=AB．AB垂直地面 O′B于点B，A′B′垂直地面O′B于点C，吊臂长度OA′=OA=10米，且cosA，sinA′．求此重物在水平方向移动的距离BC．

（1）对抽取的30株水稻稻穗谷粒数进行统计分析，请补全下表中空格，并完善直方图：

（2）如图所示的扇形统计图中，扇形A对应的圆心角为　 　度，扇形B对应的圆心角为　　度；

（3）该试验田中大约有3000株水稻，据此估计，其中稻穗谷粒数大于或等于205颗的水稻有多少株？

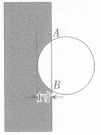
A.13B.24C.26D.28

【题目】如图，在平面直角坐标系中，点O是原点，矩形OABC的顶点A在x轴的正半轴上，顶点C在y的正半轴上，点B的坐标是（5，3），抛物线经过A、C两点，与x轴的另一个交点是点D，连接BD．

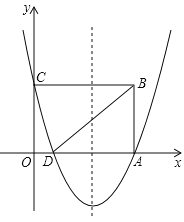
（1）求抛物线的解析式；

（2）点M是抛物线对称轴上的一点，以M、B、D为顶点的三角形的面积是6，求点M的坐标；

（3）点P从点D出发，以每秒1个单位长度的速度沿D→B匀速运动，同时点Q从点B出发，以每秒1个单位长度的速度沿B→A→D匀速运动，当点P到达点B时，P、Q同时停止运动，设运动的时间为t秒，当t为何值时，以D、P、Q为顶点的三角形是等腰三角形？请直接写出所有符合条件的值．

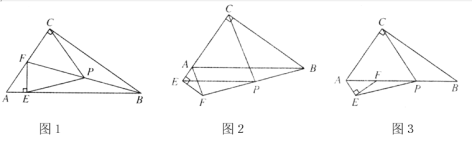
(1) 如图1，若点E，F分别落在边AB，AC上，求证：PC＝PE；

(2) 如图2，把图1中的△AEF绕着点A顺时针旋转，当点E落在边CA的延长线上时，探索PC与PE的数量关系，并说明理由．

(3) 如图3，把图2中的△AEF绕着点A顺时针旋转，点F落在边AB上．其他条件不变，问题(2)中的结论是否发生变化？如果不变，请加以证明；如果变化，请说明理由．

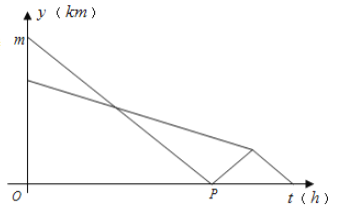
(1) 图中m＝___________，P点坐标为___________；

(2) 求汽车第一次行驶到B地时，汽车行驶路程y(km)与行驶时间t(h)的函数关系式；

(3) 求先遣分队的步行速度；

(4) 先遣分队比大部队早出发多少小时？

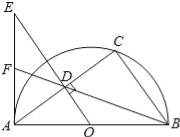
（1）求证：AEBC=ADAB；

（2）若半圆O的直径为10，sin∠BAC=，求AF的长．

根据图中提供的信息，解答下列问题：

（1）a= ，b= ；

（2）该校八年级学生共有600人，则该年级参加足球活动的人数约 人；

（3）该班参加乒乓球活动的5位同学中，有3位男同学（A，B，C）和2位女同学（D，E），现准备从中选取两名同学组成双打组合，用树状图或列表法求恰好选出一男一女组成混合双打组合的概率．

【题目】如图，抛物线y＝+bx+c经过△ABC的三个顶点，其中点A（0，﹣1），点B（9，﹣10），AC∥x轴，点P是直线AC上方抛物线上的动点．

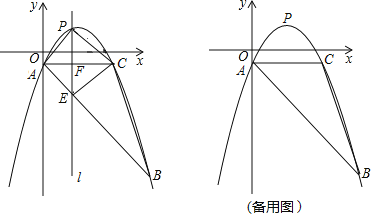
（1）求抛物线的解析式；

（2）过点P且与y轴平行的直线l与直线AB，AC分别交于点E，F，当四边形AECP的面积最大时，求点P的坐标；

（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C，P，Q为顶点的三角形与△ABC相似？若存在，求出点Q的坐标；若不存在，请说明理由．

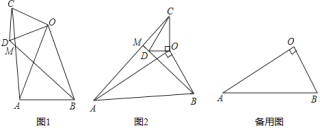
【题目】（1）问题发现:如图（1），在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝36°，连接AC，BD交于点M．①的值为　 　；②∠AMB的度数为　 　；

（2）类比探究 :如图（2），在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC，交BD的延长线于点M．请计算的值及∠AMB的度数．

（3）拓展延伸:在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M．若OD＝1，OB＝，请直接写出当点C与点M重合时AC的长．