
科目: 来源: 题型:
【题目】已知,如图,二次函数![]() (其中
(其中![]() ,
,![]() 是常数,
是常数,![]() 为正整数)
为正整数)
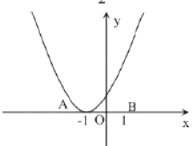
(1)若![]() 经过点
经过点![]() 求
求![]() 的值.
的值.
(2)当![]() ,若
,若![]() 与
与![]() 轴有公共点时且公共点的横坐标为非零的整数,确定
轴有公共点时且公共点的横坐标为非零的整数,确定![]() 的值;
的值;
(3)在(2)的条件下将![]() 的图象向下平移
的图象向下平移![]() 个单位,得到函数图象
个单位,得到函数图象![]() ,求
,求![]() 的解析式;
的解析式;
(4)在(3)的条件下,将![]() 的图象在
的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新的图象
轴翻折,图象的其余部分保持不变,得到一个新的图象![]() ,请结合新的图象解答问题,若直线
,请结合新的图象解答问题,若直线![]() 与
与![]() 有两个公共点时,请直接写出
有两个公共点时,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】有甲,乙两个电子团队整理一批电脑数据,整理电脑的台数为![]() (台)与整理需要的时间
(台)与整理需要的时间![]() 之间关系如下图所示,请依据图象提供的信息解答下列问题:
之间关系如下图所示,请依据图象提供的信息解答下列问题:
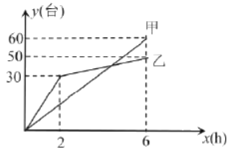
(1)乙队工作![]() 小时整理_____台电脑,工作
小时整理_____台电脑,工作![]() 时两队一共整理了_______台;
时两队一共整理了_______台;
(2)求甲、乙两队![]() 与
与![]() 的关系式.
的关系式.
(3)甲、乙两队整理电脑台数相等时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】完全平方公式是初中数学的重要公式之一:![]() ,完全平方公式既可以用来进行整式计算又可以用来进行分解因式,在学习中芳芳同学发现
,完全平方公式既可以用来进行整式计算又可以用来进行分解因式,在学习中芳芳同学发现![]() 也可以用完全平方公式进行分解因式,
也可以用完全平方公式进行分解因式,![]() ;根据以上发现解决问题
;根据以上发现解决问题
(1)写出一个上面相同的式子,并进行分解因式;
(2)若![]() ,请用
,请用![]() ,
,![]() 表示
表示![]() ,
,![]()
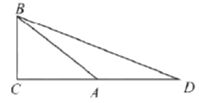
(3)如图在![]() 中,
中,![]() ,
,![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,求
,求![]() 的长(参考上面提供的方法把结果进行化简)
的长(参考上面提供的方法把结果进行化简)
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的口袋中放入![]() 个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为
个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为![]() 、
、![]() 、
、![]() 克,已知随机的摸出一个鸡蛋,摸到
克,已知随机的摸出一个鸡蛋,摸到![]() 克和
克和![]() 克的鸡蛋的概率是相等的.
克的鸡蛋的概率是相等的.
(1)求这四个鸡蛋质量的众数和中位数
(2)小明做实验需要拿走一个鸡蛋,芳芳在小明拿走后从剩下的三个鸡蛋中随机的拿走一个
①通过计算分析小明拿走一个鸡蛋后,剩下的三个鸡蛋质量的中位数是多少?
②假设小明拿走的鸡蛋质量为![]() 克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是
克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是![]() 克的鸡蛋的概率?
克的鸡蛋的概率?
查看答案和解析>>
科目: 来源: 题型:
【题目】小盛和丽丽在学完了有理数后做起了数学游戏
(1)规定用四个不重复(绝对值小于![]() )的正整数通过加法运算后结果等于
)的正整数通过加法运算后结果等于![]()
小盛:![]() ;丽丽:
;丽丽:![]() ,问是否还有其他的算式,如果有请写出来一个,如果没有,请简单说明理由;
,问是否还有其他的算式,如果有请写出来一个,如果没有,请简单说明理由;
(2)规定用四个不重复(绝对值小![]() )的整数通过加法运算后结果等
)的整数通过加法运算后结果等![]()
小盛:![]() ;丽丽:
;丽丽:![]() ;请根据要求再写出一个与他们不同的算式.
;请根据要求再写出一个与他们不同的算式.
(3)用(2)中小盛和丽丽的算式继续排列下去组成一个数列,使相邻的四个数的和都等于![]() ,小盛:
,小盛:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
丽丽:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
则![]() ______;
______;![]() _______.求丽丽写出的数列的前
_______.求丽丽写出的数列的前![]() 项的和.
项的和.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一边长为![]() 的等边
的等边![]() 游乐场,某人从边
游乐场,某人从边![]() 中点
中点![]() 出发,先由点
出发,先由点![]() 沿平行于
沿平行于![]() 的方向运动到
的方向运动到![]() 边上的点
边上的点![]() ,再由
,再由![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,又由点
,又由点![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,则此人至少要运动_______
,则此人至少要运动_______![]() ,才能回到点
,才能回到点![]() .如果此人从
.如果此人从![]() 边上意一点出发,按照上面的规律运动,则此人至少走______
边上意一点出发,按照上面的规律运动,则此人至少走______![]() ,就能回到起点.
,就能回到起点.
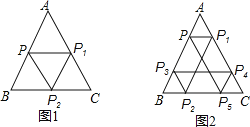
查看答案和解析>>
科目: 来源: 题型:
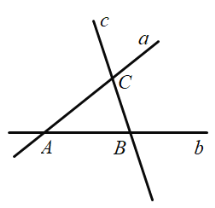
【题目】某地为了促进旅游业的发展,要在如图所示的三条公路![]() ,
,![]() ,
,![]() 围成的一块地上修建一个度假村,要使这个度假村到
围成的一块地上修建一个度假村,要使这个度假村到![]() ,
,![]() 两条公路的距离相等,且到
两条公路的距离相等,且到![]() ,
,![]() 两地的距离相等,下列选址方法绘图描述正确的是( )
两地的距离相等,下列选址方法绘图描述正确的是( )
A.画![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,两线的交点符合选址条件
的垂直平分线,两线的交点符合选址条件
B.先画![]() 和
和![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,三线的交点符合选址条件
的垂直平分线,三线的交点符合选址条件
C.画三个角![]() ,
,![]() 和
和![]() 三个角的平分线,交点即为所求
三个角的平分线,交点即为所求
D.画![]() ,
,![]() ,
,![]() 三条线段的垂直平分线,交点即为所求
三条线段的垂直平分线,交点即为所求
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)课本情境:如图,已知矩形AOBC,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动,出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P,Q两点的距离为多少?当运动时间为4s时,P,Q两点的距离为多少?
(3)拓展应用:若点P沿着AO→OC→CB移动,点P,Q分别从A,C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间△POQ的面积为12cm2?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com