
科目: 来源: 题型:
【题目】如图,一次函数y=![]() x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
x﹣2的图象与x轴交于点A,与y轴交于点B,点D的坐标为(﹣1,0),二次函数y=ax2+bx+c(a≠0)的图象经过A,B,D三点.
(1)求二次函数的解析式;
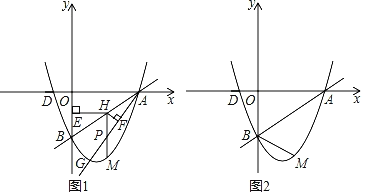
(2)如图1,已知点G(1,m)在抛物线上,作射线AG,点H为线段AB上一点,过点H作HE⊥y轴于点E,过点H作HF⊥AG于点F,过点H作HM∥y轴交AG于点P,交抛物线于点M,当HEHF的值最大时,求HM的长;
(3)在(2)的条件下,连接BM,若点N为抛物线上一点,且满足∠BMN=∠BAO,求点N的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.
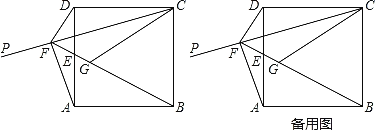
(1)试判断DF与BF的位置关系,并说明理由;
(2)若CF=4![]() ,DF=2,求AE的长;
,DF=2,求AE的长;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】大邑县某汽车出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨25%.据统计,淡季该公司平均每天有10辆货车未出租,日租金总收入为3200元;旺季所有的货车每天能全部租出,日租金总收入为6000元.
(1)求该出租公司这批对外出租的货车共有多少辆?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其它因素,该出租公司的日租金总收入最高是多少元?当日租金总收入最高时,每天出租货车多少辆?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=9,AD=6,点O为对角线AC的中点,点E在DC的延长线上且CE=1.5,连接OE,过点O作OF⊥OE交CB延长线于点F,连接FE并延长交AC的延长线于点G,则![]() =_____.
=_____.

查看答案和解析>>
科目: 来源: 题型:
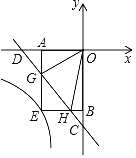
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=![]() 的解析式为_____.
的解析式为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:已知锐角∠AOC,依次按照以下顺序操作画图:
(1)在射线OA上取一点B,以点O为圆心,OB长为半径作![]() ,交射线OC于点D,连接BD;
,交射线OC于点D,连接BD;
(2)分别以点B,D为圆心,BD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接ON,MN.
根据以上作图过程及所作图形可知下列结论:①OC平分∠AON;②MN∥BD;③MN=3BD;④若∠AOC=30°,则MN=![]() ON.其中正确结论的序号是_____.
ON.其中正确结论的序号是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】110年前,中国首条自行设计和建造的铁路,京张铁路落成;110年后,在同样的地方,世界首条智能高铁京张高铁正式运行,中国速度,一直在路上,2019年底,中国高铁里程将突破3.5万公里,全世界超过![]() 的高铁轨道铺设在中国.为你骄傲,中国高铁!请将3.5万公里中的数“3.5万”用科学记数法表示为( )
的高铁轨道铺设在中国.为你骄傲,中国高铁!请将3.5万公里中的数“3.5万”用科学记数法表示为( )
A.3.5×101B.0.35×105C.35×103D.3.5×104
查看答案和解析>>
科目: 来源: 题型:
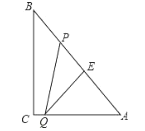
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() ,点
,点![]() 是点
是点![]() 以
以![]() 为对称中心的对称点,点
为对称中心的对称点,点![]() 运动的同时,点
运动的同时,点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() ,当点
,当点![]() 到达顶点
到达顶点![]() 时,
时,![]() 同时停止运动,设
同时停止运动,设![]() 两点运动时间为
两点运动时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)四边形![]() 面积能否是
面积能否是![]() 面积的
面积的![]() ?若能,求出此时
?若能,求出此时![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() 为等腰三角形?(直接写出结果)
为等腰三角形?(直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出:如何将一个长为17,宽为1的长方形经过剪一剪,拼一拼,形成一个正方形.(下列所有图中每个小方格的边长都为1,剪拼过程中材料均无剩余)
问题探究:我们从长为5,宽为1的长方形入手.
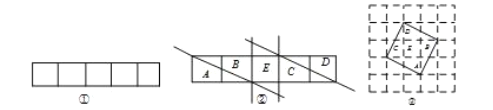
(1)如图①是一个长为5,宽为1的长方形.把这个长方形剪一剪、拼一拼后形成正方形,则正方形的面积应为_____________,设正方形的边长为![]() ,则
,则![]() _________;
_________;
(2)我们可以把有些带根号的无理数的被开方数表示成两个正整数平方和的形式,比如![]() .类比此,可以将(1)中的
.类比此,可以将(1)中的![]() 表示成
表示成![]() _____________;
_____________;
(3)![]() 的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为
的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为![]() ;类比此,(2)中的
;类比此,(2)中的![]() 可以理解为以长度________和__________为直角边的直角三角形斜边的长;
可以理解为以长度________和__________为直角边的直角三角形斜边的长;
(4)剪一剪:由(3)可画出如图②的分割线,把长方形分成![]() 五部分;
五部分;
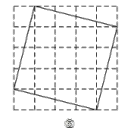
(5)拼一拼:把图②中五部分拼接得到如图③的正方形;
问题解决:仿照上面的探究方法请把图④中长为17,宽为1的长方形剪一剪,在图⑤中画出拼成的正方形.(说明:图④的分割过程不作评分要求,只对图⑤中画出的最终结果评分)
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com