
科目: 来源: 题型:
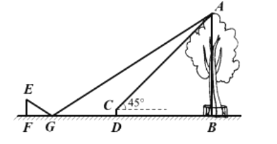
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
查看答案和解析>>
科目: 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
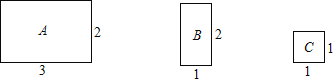
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
科目: 来源: 题型:
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:
表示,共分成四组:![]() .
.![]()
![]() .
.![]() C.
C.![]() D.
D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
八年级10名学生的竞赛成绩在![]() 组中的数据是:94,90,94
组中的数据是:94,90,94
八年级抽取的学生竞赛成绩扇形统计图:
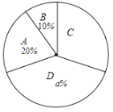
七、八年级抽取的学生竞赛成绩统计表:
年级 | 七年级 | 八年级 |
平均数 |
| 92 |
中位数 | 93 | 94 |
众数 | 99 | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中![]() 的值;
的值;
(2)根据以上数据,你认为该校七、八年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(![]() )的学生人数是多少?
)的学生人数是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】2020春节期间,一场突如其来的新冠肺炎疫情牵动着全国人民的心,因疫情发展迅速,全国口罩防护用品销售量暴涨、供应紧张,国有疫,我有责,在特殊时期,某集团紧急启动了应急响应机制,取消了工人休假,与疫情救灾相关的口罩、防护服生产线连续24小时运转,将援驰武汉的120万片口罩和8万防护服第一时间发往武汉,其中120万用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
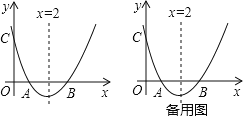
(1)求抛物线的函数表达式;
(2)设D为抛物线的顶点,连接DA、DB,试判断△ABD的形状,并说明理由;
(3)设P为对称轴上一动点,要使PC﹣PB的值最大,求出P点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
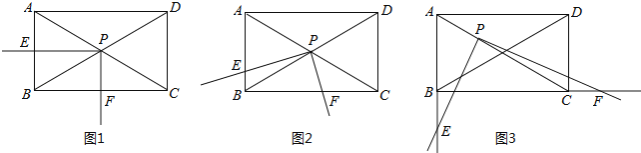
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
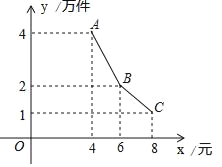
【题目】为了支持大学生创业,某市政府出台了一项优惠政策:提供10万元的无息创业贷款.小王利用这笔贷款,注册了一家淘宝网店,招收5名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款.已知该产品的成本为每件4元,员工每人每月的工资为4千元,该网店还需每月支付其它费用1万元.该产品每月销售量y(万件)与销售单价x(元)万件之间的函数关系如图所示.
(1)求该网店每月利润w(万元)与销售单价x(元)之间的函数表达式;
(2)小王自网店开业起,最快在第几个月可还清10万元的无息贷款?
查看答案和解析>>
科目: 来源: 题型:
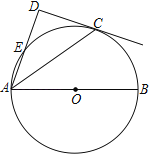
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)连接BC,若cos∠CAD=![]() ,⊙O的半径为5,求CD、AE的值.
,⊙O的半径为5,求CD、AE的值.
查看答案和解析>>
科目: 来源: 题型:
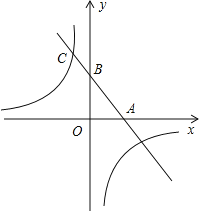
【题目】如图,一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=﹣![]() 的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
(1)求点C的坐标及k、b的值.
(2)求出一次函数图象与反比例函数图象的另一个交点的坐标,并直接写出当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com