
科目: 来源: 题型:
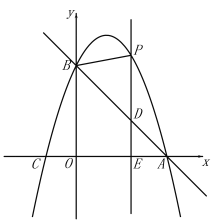
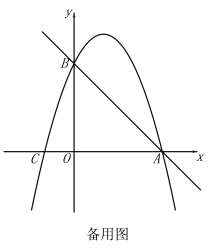
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过A,B.
经过A,B.
(1)求抛物线解析式;
(2)E(m,0)是x轴上一动点,过点E作![]() 轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
①点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标;
②点E在x轴的正半轴上运动,若![]() ,请直接写出m的值.
,请直接写出m的值.
查看答案和解析>>
科目: 来源: 题型:
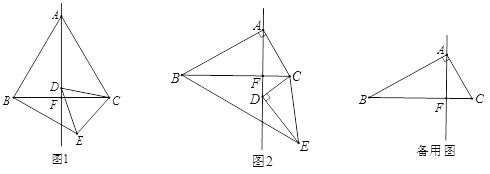
【题目】(1)问题发现:如图1,在△ABC中和△DCE中,![]() ,
,![]() ,
,![]() ,点D是BC的垂线AF上任意一点.填空:
,点D是BC的垂线AF上任意一点.填空:
①![]() 的值为 ;
的值为 ;
②∠ABE的度数为 .
(2)类比探究:如图2,在△ABC中和△DCE中,![]() ,
,![]() ,点D是BC的垂线AF上任意一点.请判断
,点D是BC的垂线AF上任意一点.请判断![]() 的值及∠ABE的度数,并说明理由;
的值及∠ABE的度数,并说明理由;
(3) 拓展延伸:在(2)的条件下,若![]() ,
,![]() ,请直接写出BE的长.
,请直接写出BE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校准备购进一批红外线测温仪和口罩若干包.已知购买1个红外线测温仪和2包口罩共需460元;购买2个红外线测温计和3包口罩共需880元.
(1)求一个红外线测温仪和一包口罩的售价各是多少元;
(2)学校准备购进红外线测温仪20个,口罩若干包(超过30包).某药店对这两种商品给出优惠活动,活动一:购买1个红外线测温仪送1包口罩;活动二:购买口罩30包以上,超出的部分按售价的五折优惠,红外线测温仪不打折.
①设购买口罩x包,选择活动一的总费用为![]() 元,选择活动二的总费用为
元,选择活动二的总费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与x的函数关系式;
与x的函数关系式;
②学校购买口罩的包数x在什么范围内,选择优惠活动一比活动二更省钱?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
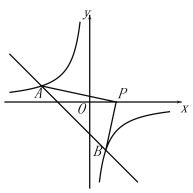
【题目】如图,如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点A(m ,1)和B (1,
的图象交于点A(m ,1)和B (1,![]() ).
).
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点P是x轴正半轴上一点,连接AP,BP.当△ABP是直角三角形时,求出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
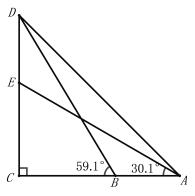
【题目】某数学兴趣小组学过锐角三角函数后,到市龙源湖公园测量塑像“夸父追日”的高度,如图所示,在A处测得塑像顶部D的仰角为45°,塑像底部E的仰角为30.1°,再沿AC方向前进10m到达B处,测得塑像顶部D的仰角为59.1°.求塑像“夸父追日”DE高度.(结果精确到0.1m.参考数据:sin30.1°≈0.50,cos30.1°≈0.87,tan30.1°≈0.58,sin59.1°≈0.86,cos59.1°≈0.51,tan59.1°≈1.67)

查看答案和解析>>
科目: 来源: 题型:
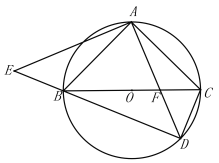
【题目】如图,在△ABC中,![]() ,BC为
,BC为![]() 的直径,D为
的直径,D为![]() 任意一点,连接AD交BC于点F,EA⊥AD交DB的延长线于E,连接CD.
任意一点,连接AD交BC于点F,EA⊥AD交DB的延长线于E,连接CD.
(1)求证:△ABE≌△ACD;
(2)填空:①当∠CAD的度数为 时,四边形ABDC是正方形;
②若四边形ABDC的面积为4,则AD的长为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】某校七、八年级各有300名学生,近期对他们“2020年新型冠状病毒”防治知识进行了线上测试,为了了解他们的掌握情况,从七、八年级各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息:
a.七年级的频数分布直方图如下(数据分为5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):

b.七年级学生成绩在80≤x<90的这一组是:
80 80.5 81 82 82 83 83.5 84
84 85 86 86.5 87 88 89 89
c.七、八年级学生成绩的平均数、中位数、众数如下:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 85.3 | m | 90 |
八年级 | 87.2 | 85 | 91 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)在随机抽样的学生中,防治知识成绩为84分的学生,在 年级排名更靠前,理由是 ;
(3)若各年级防治知识的前90名将参加线上防治知识竞赛,预估七年级分数至少达到 分的学生才能入选;
(4)若85分及以上为“优秀”,请估计七年级达到“优秀”的人数.
查看答案和解析>>
科目: 来源: 题型:
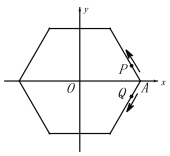
【题目】如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为( )
A.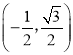 B.
B.![]() C.
C. D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在△ABC中,![]() ,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是( )
,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是( )
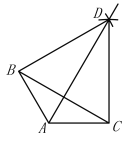
A.![]() B.△BCD是等边三角形
B.△BCD是等边三角形
C.AD垂直平分BCD.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
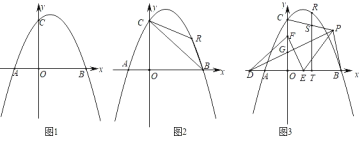
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com